Harmonisk svängningsrörelse Simple Harmonic Motion (SHM)

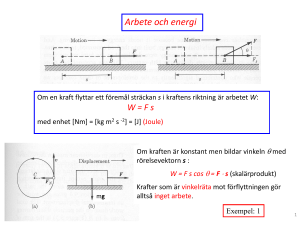
Harmonisk svängningsrörelse
Simple Harmonic Motion (SHM)
x̂
Den återförande kraften är F  kxxˆ vilket ger kraftekvationen:
d 2x
d 2x
d 2x
2
xˆ led : max  m 2  kx
m 2  kx  0


x0
2
dt
dt
dt
med lösning
x  A cos(t   ) (eller x  A sin(t   ) )
om vi kallar  2 = k/m
A är svängningens amplitud
P = 2p / är periodtiden
f = 1/P är frekvensen
( t + ) är fasvinkeln där faskonstanten  ger x värdet för t = 0 .
1
Position, hastighet och acceleration i SHM
x  A cos(t   )
v
dx
p
 Asin(t   )  A cos(t    )
dt
2
dv
a    2 A cos(t   )   2 x
dt
Hastighet v
Läge x
x, v och a representerad med
roterande vektorer. Rotationen är
moturs, värdet läses på X-axeln
cos() = sin( + p/2)
sin() = cos( - p/2)
Acceleration a
-cos() = cos(+ p)
-sin() = sin(+ p)
Exempel: 1
2
Kinetisk energi vid harmonisk svängningsrörelse
1 2 1
Ek  mv  m 2 A2 sin 2 (t   )
2
2
använd sin 2   1  cos2  och x  A cos(t   ) ger
1
1
1
Ek  m 2 A2 1  cos2 (t   )  m 2 A2  x2  k A2  x 2
2
2
2






Det sista uttrycket är identiskt med det som tidigare tagits fram
genom att integrera fjäderkraften. Det framgår att:
Vid SHM är kinetiska energin maximal för x = 0 och 0 vid vändlägena, x
=A
3
Potentiell energi vid harmonisk svängningsrörelse
Den potentiella energin erhålls ur sambandet :
dEp/dx = F = kx
Etot
vilket ger
Ep = (1/2)kx2 om Ep = 0 för x = 0.
Etot = Ek + Ep = (1/2)k(A2 - x2)+ (1/2)kx2 = (1/2)kA2
Totalenergin Etot är alltid konstant och växlar mellan potentiell och kinetisk
energi.
Exempel: 2
4
Exempel: Pendel
Exempel: 3
5
Anharmonisk svängning
Här gäller ej att Ep = (1/2)k(xx0)2 vilket leder till att
svängningen blir assymetrisk och att frekvensen beror av
amplituden.
För små svängningar kring jämviktsläget x0 är ändå SHM en
god approximation vilket framgår om potentiella energin
kring x0 Taylor utvecklas:
= 0 ty x0 min
dE
E p  E p ( x0 )  p
dx
2
1 d Ep
x0 x  x0  
2 dx2
=k>0
2
3




x

x

O
x

x
x
0
0
0
Ep(x)  konstant + (1/2)k(x - x0)2
Dvs: vi har i allmänhet SHM för små svängningar
För stora utslag kan t.ex. en dämpad pendel utsatt för oscillerande kraft ge irreguljär,
kaotisk rörelse. Närliggande startvärden ger helt olika slutvärden.
Exempel: 4
6
Dämpade svängningar
I en mer realistisk modell av svängningsrörelse har vi även en
bromsande term pga friktion (t.ex. luftmotstånd). Vanligast är att
friktionskraften skrivs:
F = lv = l (dx/dt)
dx 
d 2x

Ftot    kx  l   m 2
dt 
dt

d 2 x l dx k

 x0
2
dt m dt m
Lösning: x(t )  Cer1t  Der2t där r1,2 är lösn. till karakteristiska ekv.
l
k
l
 l  k
r2  r   0  r  
   
m m
2m  2m  m

2
2

x(t )  et  C ei

där   02   2
02  2
t  D ei
02  2
02
Om 2 < 02
(svag dämpning)
t   Aet cos t  

7
Dämpade svängningar
x(t )  Aet cos t  
Dämpad svängning:
1)
Amplituden minskar med tiden
2)
Frekvensen lägre än för det odämpade fallet
  02   2
Exempel: 5
8