Inroduktion till vektorer
advertisement

Inroduktion till vektorer
Mikael Forsberg
January 21, 2004
1
Skalärer och de reella talen
Vi har många talsystem, t.ex, de naturliga talen N = {1, 2, 3, . . . }, de hela talen
Z och de rationella talen Q = { ab : a, b ∈ Z}. Dessa talsystem ligger alla på
den reella tallinjen men för att göra den fullständig så måste man spackla igen
hålen i de rationella talen. Gör man detta ordentligt så har vi de reella talen.
I den här kursen så kommer vi kalla de reella talen för skalärer, ett ord
man brukar förknippa med så kallade skalära storheter som längd tid, fart och
strömstyrka. De skalära storheterna ska inte blandas samman med vektoriella
storheter som hastighet, kraft och rörelsemängdsmoment, som förutom storlek
även har en riktning. I den här kursen lär vi oss “allt” om vektorer, vilket är
vad vi nu fortsätter med.
2
Det reella n-dimensionella rummet Rn
De flesta av oss är förmodligen bekant med xy−planet. Detta består av alla
reella talpar: R2 = {(x, y) : x, y ∈ R}. Det tredimensionella rummet R3 består
på motsvarande sätt av alla reella taltripplar (x, y, z).
Det reella n-dimensionella rummet är en generalisering av dessa två och
tre-dimensionella rella rummen:
Rn = {(x1 , . . . , xn ) : xj ∈ R, j = 1, . . . , n}
Om n = 2 resp. n = 3 så har vi R2 respektive R3 . Om n = 1 så är detta vår
vanliga reella tallinje, men detta kommer vi inte att tänka så mycket på.
2.1
Räkneregler för Rn
Vi sammanställer här de räkneregler som gäller för de flerdimensionella reella
rummen. Räknereglerna gäller visserligen även för de reella talen, men egenskaperna för de reella talen beskrivs bäst på annat vis. Den som vill kan fördjupa
sig i detta på egen hand. (Med ett högre matematiskt språk säger man att de
reella talen bildar en kropp medan de andra endast är vektorrum)
Vi definierar först addition och multiplikation med skalär
1
Definition 2.1. Addition av två n-tuppler sker komponentvis:
(x1 , . . . , xn ) + (y1 , . . . , yn ) = (x1 + y1 , . . . , xn + yn )
Vid multiplikation med skalär multipliceras en n-tuppel med ett reellt tal. Multiplikationen sker komponentvis, dvs varje komponent multipliceras med talet:
a(x1 , . . . , xn ) = (ax1 , . . . , axn ).
Anmärkning 2.2. Språklig not: På engelska kalar man multiplikation med skalär
för scalar multiplication. På svenska säger vi inte skalär multiplikation i detta
fall eftersom detta uttryck reserveras för den multiplikation som på engelska
kallas för dot product (en produkt av två vektorer som blir en skalär)
Theorem 2.3. I det n-dimensionella reella rummet gäller följande räkneregler:
Låt x, y och z vara n-tuppler och a och b skalärer. Då gäller
A1. x + y är en n-tuppel. (Rn sluten under addition)
A2. x + y = y + x. (Additionen är kommutativ)
A3. x + (y + z) = (x + y) + z. (Additionen är associativ.)
A4. Det finns en n-tuppel 0 så att x + 0 = 0 + x = x (0 = (0, . . . , 0) kallas den
additiva identiteten.)
A5. För alla n-tuppler x så finns en n − tuppel −x så att x + (−x) = 0. (
Varje n-tuppel har en additiv invers.)
S1. ax är en n-tuppel. ( Rn sluten under multiplikation med skalär.)
S2. a(x + y) = ax + ay. (första distributiva egenskapen)
S3. (a + b)x = ax + bx . (andra distributiva egenskapen)
S4. a(bx) = (ab)x. (multiplikation med skalär är associativ)
S5. 1x = 1 (identitet för multiplikation med skalär)
Notera att dessa är precis axiomen för vektorrum på sidan 189-190 i Nicholson. Vi kommer att se, så småning om, att de reella rummen står modell för
de allmänna vektorrumen. Faktiskt är att genom att införa en så kallad bas i
vektorrummen så kan man överföra vektorrummen till ett lämpligt reellt rum.
(Åtminstone för vektorrum med ändlig dimension, rum med oändlig dimension,
t.ex. så kallade funktionsrum behandlas inte i denna kurs utan här hänvisas
läsaren till funktionalanalysen)
2
3
Vektorer
Definition 3.1. Vi definierar begreppet vektor och addition av vektorer:
• En vektor är ett objekt som har både längd och riktning.
• En vektor är förändras inte vid parallellförflyttning eftersom riktningen
och längden är den samma efter en sådan operation.
• Vektorer ritas ofta som pilar. Pilens startpunkt kallas fotpunkt och dess
slutpunkt för spets.
• Geometrisk addition betyder att man parallellförflyttar pilar så att man
bildar en kedja av pilar. Summan av vektorerna blir då en pil som går
från fotpunkten av den första pilen i kedjan till spetsen på den sista pilen
i kedjan.
4
Punkter i Rn ↔ n-dimensionella vektorer
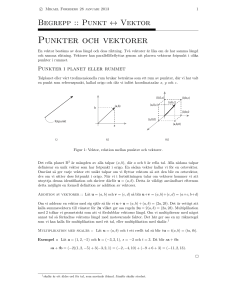
Betrakta figur 1
x=(a,b)
y=(c,d)
u=ox
v
Figure 1: Punkter i R2 är vektorer och tvärt om.
3
Theorem 4.1. n-tuppler kan identifieras med n-dimensionella vektorer.
Proof. För varje n-tuppel x så finns det en unik ortsvektor, dvs en vektor som
har sin fotpunkt i origon och sin spets i x. Givet en vektor v så finns det en
entydig ortsvektor med samma längd och riktning som v. Denna ortsvektor
pekar på en unik n-tuppel.
Anmärkning 4.2. Tack vare sats refT:tuppelident så kan vi kalla n-tuppler för
vektorer och på så vis får vi via våra räkneregler en stark kalkylapparat för våra
vektorer.
5
Introduktion av geometri i Rn
Geometri är Grekiska och betyder “att mäta jorden”. Vi måste alltså introducera begrepp som längd och vinklar i våra rum av vektorer. Längdbegreppet är
lätt. Vi utnyttjar Pythagoras sats för sträckan mellan origo och x blir
q
||x|| = x21 + · · · + x2n
För att introducera vinklar så introducerar vi den så kallade skalärprodukten:
Definition 5.1. Skalärprodukten mellan två vektorer x och y definieras som
x • y = ||x||||y|| cos α,
(1)
där α är vinkeln mellan x och y, när de är parallellförflyttade så att de har
gemensam fotpunkt.
För att detta ska vara ett sätt att få information om vinkeln så behöver de
övriga komponenterna i (1) vara någorlunda lätta att räkna ut. Framförallt vet
vi ingenting om hur x • y kan beräknas. Vi har dock följande sats:
Theorem 5.2. Låt x = (x1 , . . . , xn ) och y = (y1 , . . . , yn ), då gäller
x • y = x1 y1 + · · · + xn yn =
n
X
xj yj
j=1
Vi återkommer till skalärprodukten när vi går igenom kapitel fyra i Nicholson.
4