prov3-Ma1a-121116-1635
advertisement

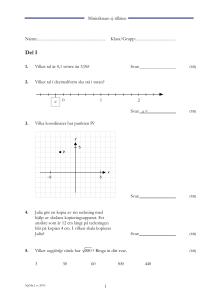
Namn: _______________________________________________________ (Lärare: Ingemar Carlsson) Anvisningar – Del B och Del D Provtid 90 minuter för Del B och Del D. Vi rekommenderar att du använder högst 30 minuter för arbetet med Del B. Du får inte börja använda digitala verktyg förrän du har lämnat in dina svar på Del B. Hjälpmedel Del B: Formelblad och linjal. Del C och D: Digitala verktyg, formelblad och linjal. Del A Muntlig del. Ges inte vid detta tillfälle. Del B Denna del består av uppgifter som ska lösas utan digitala verktyg. På några av uppgifterna krävs redovisning, som redovisas i figuren och rutan intill uppgiften. Till övriga uppgifter krävs endast svar. Efter varje uppgift anges maximala antalet poäng som du kan få för ditt svar/din lösning. Del C Denna del är en större uppgift som brukar ta längre tid. I rutan vid uppgiften står det vad läraren ska ta hänsyn till vid bedömningen. Ges inte vid detta tillfälle. Del D Denna del består av uppgifter där det om inget annat anges krävs att du • redovisar dina lösningar • förklarar/motiverar dina tankegångar • ritar figurer vid behov. Kravgränser Poängen på varje uppgift är angiven som (E/C/A). Poängen är ledtal för nivåbestämning och provbetyg. Prov på del av kursen är lätt vägande betygsunderlag. Nationellt kursprov är tungt vägande betygsunderlag. Undre gräns för provbetyget E: 1) 60% av max E. C och A-poäng får räknas. 2) Inget krav. D: 1) 60% av max E. C och A-poäng får räknas. 2) 20% av max C. A-poäng får räknas. C: 1) 70% av max E. C och A-poäng får räknas. 2) 30% av max C. A-poäng får räknas. B: 1) 70% av max E+C. A-poäng får räknas. 2) 30%¤ av max A. A: 1) 80% av max E+C. A-poäng får räknas. 2) 50% av max A. Tabellen motsvarar gränsernas nivå på nationella prov. Om C- eller A-poäng respektive A-poäng behövs för att klara 1) kravet på bredd, får inte samma poäng användas för att klara 2) kravet på djup, d v s en poäng får inte räknas två gånger. Övriga anvisningar Följ det som kommenteras av läraren innan och under provet. Det skrivs också på tavlan, ifall du var upptagen med ett problem när informationen gavs. Namn:____________________________________________________________________ DEL B. Ingen miniräknare. Skriv i ruta för redovisning av lösning eller svarsrad på detta uppgiftspapper. DEL B måste lämnas in innan du börjar på DEL D. (Detta prov har ingen DEL C) 1. (2/1/0) Skriv vardera en av a-c i decimalform och i procentform Svar: a)_______och________ a) 1/4 b)_______och_________ b) 2/5 c)_______och_________ c) 65/50 2a. Hur många procent av muggarna är mörkgrå? (1/0/0) Svar: _______________ 2b. Vilken eller vilka av följande tal betyder 40% (1/1/0) Ringa in 3. Hur stor del av figuren är grå? (2/1/0) Svar: a)____________________ Svara i a) Bråkform b) Decimalform c) Procentform b)____________________ c)____________________ 4. (0/1/0) En mobiltelefon kostar 2950 kr. priset ökar sedan med 7 % , minskar därefter med 3%, och ökar slutligen med 10%. Ringa in det eller de uttryck som är beskriver nya priset. 5. (0/1/0) a) Vad kostar det att åka 12 km? b) Hur långt kan man åka för 160 kr? 6. : b)_______________ Om –a + b = 12. Vilken/vilka av följande uttryck gäller då. Ringa in. b – a =-12 b + b –a –a = -24 7. Svar: a)_______________ -2a +2b =24 (0/1/1) -10a + 10b = 120 a = 12 - b En list har följande profil i genomskärning. Beräkna arean av den gråa ytan. (0/1/1) Svar: _______________ 8. (0/3/0) Svar: a)_______________ b)_______________ c)______________ DEL D. Med miniräknare. Fullständiga lösningar och svar. DEL B måste lämnas in innan du börjar på DEL D. (Detta prov har ingen DEL A och C) 9. Lös ekvationerna a) x + 4 = 10 (2/1/1) 𝑥 b) 4 = 0,5 c) 8x - 1 = 5x + 20 1 d) 3x =3 + 𝑥 10. Åsa, Michael och Maribel har vunnit 75 000 kr på lotto Vinsten ska delas så att Åsa får 4 gånger så mycket som Michael och Maribel ska få 6000 kr mer än Michael. Hur mycket får Åsa? (1/1/1) 11. En potatis är 6 cm lång. (1/1/1) a) Vad potatisens längd i skala 1:3 b) Vad är potatisens längd i skala 2:1 c) Potatisen skalas omsorgsfullt och skalet visar sig, när det läggs ut plant, ha en sammanlagd area på 91 cm2. Vilken skala (avrundat till heltal) har en avbildning där skalet har en area på 29 cm2 12. Förhållandet mellan pojkar och flickor i en undervisningsgrupp är 2:8. a) Hur många procent är pojkar? b) Antalet flickor ökar med 200 %. Hur många pojkar ska det vara efter ökningen om ökningen av antalet pojkar ska vara proportionell med ökningen av antalet flickor. (1/1/1) 13. Vad kallas trianglarna? Bestäm vinkeln, v, och vinkeln u. a) 14. (1/1/0) b) Hur många liter vatten rymmer en cylinder? (1/1/0) a) Då radien på bottenarean är 2,5 cm och höjden är 12 cm b) Då arean på bottenarena är 22 cm2 och höjden är 8,5 cm 15. Beskriv koncist (exakt och kortfattat) någonting som förändrar sig a) Linjärt b) Exponentiellt (0/2/0) 16. (2/4/4)