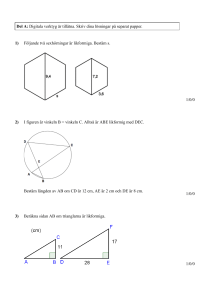
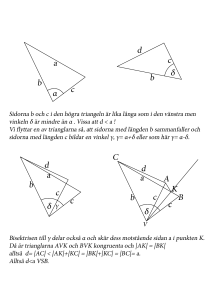
Matematikprov 1, kurs A (sida 1) Namn: Klass:

Väggaskolan
Karlshamn
17-07-15
Repetition matematik kurs A
OBS! Följande punkter samt övningsuppgifter endast ett urval av Ma A!

Räkneordning
Kom ihåg! Vid uträkningar måste en viss ordning följas:
1. Potenser 2. Parenteser 3. Multiplikationer och divisioner 4. Additioner och subtraktioner
Ex. (102+14) - 73 + 2 = (100 + 14) – 21 + 2 = 114 – 21 + 2 = 95
OBS! När du använder miniräknaren kom ihåg ”osynliga” parenteser
4  12
4  12
4  12
 3 dvs FEL!

Ex.
slår du in precis som det står kan det bli
3
3  3 (3  3)

Negativa tal
Vid alla räknesätt gäller samma minnesregel ” lika tecken ger plus, olika tecken ger minus”
Observera dock ex. (–3) – 4 = –7 . Medan 3 – (– 4) = 3 + 4 = 7.
Försök läsa skillnaden: 1:a ex. vi skall minska (minus tre) med fyra
2:a ex. minska med ett negativt tal = plus!

Parenteser
Reglerna för parentesräkning är framför allt viktiga vid algebra räkning då du inte kan räkna
ut vad som står inne i parentesen t.ex. (x + 3)
1. ex. 2 + (x – 3) = 2 + x – 3 (plus framför = ta bort utan att ändra något)
2. ex. 2 – (x – 3) = 2 – x + 3 (minus framför = ta bort och ändra tecken i parentes)
3. ex. 2(x – 3) = (2x – 2 3) (tal multiplicerat med parentes mult. med alla tal i ( ):en )
--------------------------------------------------------------------------------------------------------------1. Beräkna
2. Förenkla
(2 + 3) – (7 – 12) + 4 ( 3 + 6) = ……………………………………..
(2 + x) – (7 – x) + 4 (x + 6) = ……………………………………….
-------------------------------------------------------------------------------------------------------------- Potenser
23 betyder 2 2 2 dvs två multiplicerat med sig själv tre gånger, 2 kallas bas och 3 kallas
exponent, tillsammans bildar de en potens. Detta skrivsätt ger några räkneregler samt
definitioner enligt nedan, kom dock ihåg att basen måste vara samma för att de ska gälla
- 34 35 = 34+5 = 39
(multiplikation, addera exponenterna)
- 46 / 42 = 46 –2 = 44
(division, subtrahera exponenterna)
2 3
2 3
6
- (2 ) = 2 = 2
(potens upphöjd med att tal, multiplicera exponenterna)
Reglerna ger följande speciella definitioner
- 20 = 1 , 60 = 1 osv.
ALLA potenser med exponenten noll blir ETT!
1
1
1
 ) dvs en negativ exponent ger bråk med positiv exponent enl. ex.
- 3 –2 = 2 (
33 9
3
--------------------------------------------------------------------------------------------------------------32  34
3. Förenkla (skriv som en potens)
= ………………………
33
---------------------------------------------------------------------------------------------------------------
Väggaskolan
Karlshamn

17-07-15
Grundpotensform
Alla tal kan skrivas som ett ental multiplicerat med en tiopotens vilket underlättar när man
har mycket stora och mycket små tal.
Ex. 7700 = 7,7  103
(trean kan här tolkas som att man skall flytta decimaltstrecket 3 steg
åt höger för att få 7700 från 7,7)
-2
Ex 0,0413= 4,13 10
(-2 kan här tolkas som att flytta decimalstrecket 2 steg åt vänster)
--------------------------------------------------------------------------------------------------------------Skriv som grundpotensform
4. a) 4500 =………. b) 0,0034 = ………. c) 16 200 000 = ………. d) 0,00003 = ………..
Skriv som decimaltal alternativ heltal
5. a) 1,3 104 = ……………. b) 3,2 10-5 = …………… c) 1,456 108 = ………………
-------------------------------------------------------------------------------------------------------------- Procent
Det räcker i princip att kunna följande 3 basproblem för att räkna med procent.
1. Beräkna procenten. Ex. 42 av 234 är 42/234 0,18 = 18%, 76 av 32 är 76/32 2,38=238%
2. Beräkna ”delen”. Ex 31% av 129 = 0,31  129  40
3. Beräkna ”hela”. 21% är 45, 1% är 45/21, 100% dvs ”hela” blir(45/21)100  214
--------------------------------------------------------------------------------------------------------------6. Beräkna 22% av 258 kr = ………………………….
7. En klass hade 8 flickor och 15 pojkar. Hur många procent var flickor? …………………….
-------------------------------------------------------------------------------------------------------------- Förändringsfaktor
Att räkna en procentuell förändring görs enklast med förändringsfaktor dvs man multiplicerar
med det tal som ger vad som skall vara kvar.
Ex. 120 ökar med 10% till 1,1 120 = 132 där 1,1 kan tolkas som 110% (100%+10%)
Ex 120 minskar med 10% till 0,9 120 = 108 där 0,9 kan tolkas som 90% (100%-10%)
Förändringsfaktorn kan erhållas genom att dela det nya värdet med det gamla eftersom det är
samma sak som att beräkna hur många procent det nya är av det gamla.
Ex. Gammalt pris 129 kr, nytt pris 149 kr. Förändringsfaktor = 149/1291,16 dvs ökning
16%
Ex. Gammalt pris 149 kr, nytt pris 129 kr. Förändringsfaktor = 129/1490,87
dvs minskning 13% (från 100% till 87%)
Ex Gammalt pris 49 kr, nytt pris 129 kr. Förändringsfaktor =129/492,63 dvs ökning 163%
(från 100% till 263%)
--------------------------------------------------------------------------------------------------------------8. Beräkna med förändringsfaktor nytt pris om priset ökar med 25% från 79 kr.
9. Beräkna med förändringsfaktor nytt pris om priset minskar med 35% från 169 kr.
10. Beräkna med förändringsfaktor den procentuella förändringen om priset ändras från 269kr
till 299 kr.
11. Beräkna med förändringsfaktor den procentuella förändringen om priset ändras från 169kr
till 99 kr.
---------------------------------------------------------------------------------------------------------------
Väggaskolan
Karlshamn

17-07-15
Skala
Skalan kan anges på många olika sätt, det vanligaste är t.ex 1:10 000 eller 5:1. Det första
innebär en förminskning med 10 000 ggr och det andra en förstoring med 5 ggr.
Kom dock ihåg att skala på exempelvis en karta är längdskala vilket inte innebär att arean
ökar med denna skala utan med skalan i kvadrat. Enhetsbyten blir nödvändiga att behärska,
t.ex. 12 dm2=1200 cm2.

Likformiga trianglar
Om två trianglar är likadana sånär som på skalan så kallas trianglarna för likformiga och
förhållandet mellan likbelägna sidor i de olika trianglarna är lika.
Ex. 8
8
6
6
x
6  12

x
9
8 12
8
12
x
För att kunna säga att två trianglar är likformiga räcker det att se att trianglarna har två
vinklar som är lika stora. Den tredje blir automatiskt lika då summan av vinklarna är 180
--------------------------------------------------------------------------------------------------------------12. En karta är ritad i skala 1: 100 000. Hur långt är 2 cm på kartan i verkligheten?
13. Beräkna sidan markerad med ett x.
(trianglarna är likformiga!)
10
6
14
x
8
-------------------------------------------------------------------------------------------------------------- Geometri
I geometri handlar det ofta om att kunna känna igen vilket samband som ska användas för att
bestämma t.ex. arean eller volymen för ett föremål. Ofta kan man behöva dela upp en figur i
olika områden för att kunna bestämma t.ex. area. Omvandling mellan enheter är också
nödvändig att kunna.
--------------------------------------------------------------------------------------------------------------14. Beräkna omkrets och area för rinken intill.
18m
15. En tunna har höjden 1,0 meter samt en diameter på 0,8 m.
Hur många liter rymmer den?
25m
16. a) 40 cm2 = __________________ dm2
b) 0,2 m3 = __________________ dm3
--------------------------------------------------------------------------------------------------------------
Statistik
Medelvärde = summan/antalet, ex. medelålder = (summan av alla åldrar)/(antal personer)
Median =”mitten”, talen i storleksordning, medelvärdet av de två mittersta om antalet jämnt
Typvärde = ”det vanligaste värdet”, kan vara fler än en
--------------------------------------------------------------------------------------------------------------17. Vikten hos några laxar varierade enligt: 5, 6, 8, 6, 9 (kg) Medelvärde? Median?
Typvärde?
Väggaskolan
Karlshamn
17-07-15
-------------------------------------------------------------------------------------------------------------- Ekvationer
Att lösa vanliga ekvationer kräver ofta en strategi. Målet är att komma fram till x = …….
Vägen är att steg för steg göra samma sak på båda sidor likhetstecknet tills x är ensamt.
1,1x  4  5,2
1,1x  5,2  4 (lägger till 4 på bägge sidor)
1,1x  9,2
x
9,2
1,1x
 6,6 (delar båda sidor med det som står framför x) ((
 x))
1,1
1,1
Finns det flera termer innehållande x så börjar jag med att samla ihop de jag har.
x  1,2x  9  12
2,2x  9  12
2,2x  12  9
2,2x  21
21
 9,5
2,2
--------------------------------------------------------------------------------------------------------------Lös ekvationerna
x
18. a) 1,6x + 4 = 13,2
b) 0,16x – 5 + 1,1x = 12
c) x + 45,4 – 3x = 21
--------------------------------------------------------------------------------------------------------------
Kvadratrötter
För att lösa en enkel andragradsekvation t.ex. x2 = 14 så måste man känna till kvadratroten.
Kvadratroten kallas det positiva tal som multiplicerat med sig själv ger det som står innanför
rottecknet.
Ex. 4  4 = 16 alltså 16  4 vilket ger att ekvationen x 2  9 kan lösas enligt x   9  3
OBS! –3 är också en lösning eftersom (-3)  (-3) = 9. Ofta i praktiska tillämpningar kan dock
den negativa lösningen struntas i men den bör finnas med när man löser ekvationen. För att
beräkna kvadratrötter som inte ger jämna heltal ex. 10  3,16 behövs miniräknare!!
--------------------------------------------------------------------------------------------------------------19. Lös ekvationen
a) x2 = 25
b) x2 = 31
c) 2x2 + 7 = 13
20. Bestäm sidan x i den rätvinkliga triangeln intill. 7
8
-------------------------------------------------------------------------------------------------------------- Formler och grafer
Väggaskolan
Karlshamn
17-07-15
Att kunna teckna och tolka formler används bl.a då samma beräkningar skall göras
upprepade gånger. Att dessutom kunna presentera formeln (funktionen) som en linje (graf) i
ett koordinatsystem ger ett alternativt sätt att dra slutsatser och avläsa tillhörande värden.
Ex. En kund betalar för en hyrbil ett fast pris, 399 kr, samt även 12 kr per körd mil.
Formeln blir då att den totala kostnaden, y, kan beräknas med y = 399 + 12x där x är antal
mil
För att rita formeln i ett koordinat system så gör vi en först en värdetabell. Sen när vi vet
vilka x- och y-värden vi har så konstruerar vi koordinatsystemet med x- och y-axlar.
Sist prickar vi in våra punkter (x- och
y
tillhörande y-värde) i koordinatsstemet
och
drar en linje som sammanfogar punkterna.
x
0
20
40
60
y
399 + 120 = 399
399 + 1220 = 639
399 + 1240 = 879
399 + 1260 = 1119
500
x
Observera att skalan på axlarna kan vara olika!
10
Ur grafen kan sedan andra punkter än de
beräknade avläsas ex. för x = 10 får vi y ca. 500.
--------------------------------------------------------------------------------------------------------------21. Skriv en formel som ger min månadslön om jag har 8800 kr i grundlön och 550 kr per såld
vara.
22. Rita på rutat papper graferna till formlerna (funktionerna) y = 2x och y = 10 + 4x
Väggaskolan
Karlshamn
17-07-15
FACIT/LÖSNINGSFÖRSLAG
1. (2 + 3) – (7 – 12) + 4 ( 3 + 6) = 5 – (-5) + 4·9 = 5 + 5 +36 = 46
2. (2 + x) – (7 – x) + 4 (x + 6) = 2 + x – 7 + x + 4x + 4·6 = 6x +19
32  34 36
3.
 3  36 3  33
3
3
3
4. a) 4500 =4,5·103 b) 0,0034 = 3,4·10-3 c) 16 200 000 = 1,62·107 d) 0,00003 = 3·10-5
5. a) 1,3 104 = 13 400 b) 3,2 10-5 = 0,000032 c) 1,456 108 = 145 600 000
6. 22% av 258 kr = 0,22·258 ≈ 57 kr
7. 8/23 ≈ 0,35 = 35%
8. + 25% ger förändringsfaktor 1,25 ger nytt pris 79·1,25 ≈ 99 kr.
9. - 35% ger förändringsfaktor 0,65 ger nytt pris 169·0,65 ≈ 110 kr.
10. nytt pris / gammalt = 299/269 ≈ 1,11 dvs +11%
11. nytt pris / gammalt = 99/169 ≈ 0,59 dvs -41%
12. 2 cm på kartan är 2 100 000 = 200 000 cm = 2 000 m = 2 km i verkligheten.
13. Likformighet betyder att de är lika men i olika skala! Dvs förhållandet mellan sidorna är
lika. Den stora triangeln är 1,4 ggr större (14/10) varför x = 1,4 · 6 = 8,4.
14 x
14
  x  6   8,4
Bäst är att direkt ställa upp
10 6
10
14. Studerar man figuren så ser man att den består av 2 st halvcirklar (= en hel) och en
rektangel. Arean blir därför   r 2  b  h    92  25  18  700 m2. (radien = 18/2)
Omkretsen blir cirkelns + rektangelns bredder dvs   d  2  b   18  2  25  110 m
15. En tunna är en cylinder, V    r 2  h
(1 dm3 = 1 liter) Räknar vi med dm får vi volymen i liter. V    42  10  500 liter.
16. a) 40 cm2 = 0,40 dm2
b) 0,2 m3 = 200 dm3
56869
 6,8 median = 6 (5,6, 6, 8, 9) typvärde = 6 ( 2 st 6:or)
17. medelvärde=
5
18. a) x = 9,8/1,6 = 5,75 b) x = 17/1,26 ≈ 13,5
c) x = 24,4/2 = 12,2
19. a) x1 = 5, x2 = -5 b) x   31 x1 ≈ 5,6 x2 ≈ -5,6 c) x   3 x1 ≈ 1,73 x2 ≈ -1,73
20. Pythagoras sats ger x2 = 72 + 82 som har positiv lösning x ≈ 7,5
21. y = 8800 + 550x där x är antal sålda varor och y är månadslön i kronor.
22.
y = 10+4x
y = 2x