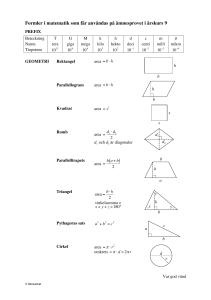
Gymnasieelevers geometrikunskaper i kursen

Linköpings universitet | Matematiska institutionen
Examensarbete, grundläggande nivå, 15 hp | Lärarprogrammet
Höstterminen 2016 | LIU-LÄR-L-EX--16/26--SE
Gymnasieelevers geometrikunskaper i
kursen Matematik 2b
– en kvalitativ innehållsanalys av elevers kompetenser och
kunskapsnivåer
Upper Secondary School Students’ Knowledge of Geometry in the Course Mathematics 2b
– A Qualitative Content Analysis of Students’ Skills and Knowledge Levels
Chau Van
Handledare: Anna Lundberg
Examinator: Björn Textorius
Linköpings universitet
SE-581 83 Linköping, Sweden
013-28 10 00, www.liu.se
Institutionen för matematik
581 83 LINKÖPING
Språk
Svenska/Swedish
Rapporttyp
Examensarbete grundnivå
Seminariedatum
2016-12-08
ISRN-nummer
LIU-LÄR-L-EX--16/26--SE
Titel: Gymnasieelevers geometrikunskaper i kursen Matematik 2b – en kvalitativ innehållsanalys av
elevers kompetenser och kunskapsnivåer
Författare: Chau Van
Sammanfattning
Studien behandlar kompetenser och kunskapsnivåer hos gymnasieelever inom
geometriavsnittet, matematikkurs 2b. Syftet är att undersöka i vilken utsträckning elever
behärskar de matematiska kompetenserna och vilken kunskapsnivå inom avsnittet geometri
elever uppnår på ett kunskapstest som konstruerats av uppgifter från nationella prov och
elevernas läromedelsbok.
Datainsamlingen genomfördes på en svensk gymnasieskola och omfattar 47 elever från två
olika klasser i årskurs 2 på det samhällsvetenskapliga programmet. Samtliga elever har besvarat
kunskapstest skriftligt. En innehållsanalys med utgångspunkt från kompetenser och
kunskapsnivåer har sedan utförts på elevernas skriftliga svar och resultatet visar att eleverna
behärskar algoritmkompetens och att en del elever behärskar begreppskompetens. Resultatet
visar också att de flesta av eleverna befinner sig på kunskapsnivå 2 och 3. Många elever saknar
således en djupare förståelse för geometrin enligt analysen med kunskapsnivåer.
Rekommendationen efter studien är att eleverna behöver mera undervisning om begreppens
definitioner för att förbättra de andra kompetenserna såsom resonemangskompetens,
modelleringskompetens och kommunikationskompetens.
Nyckelord: förmågor, geometri, gymnasieskolan, kompetenser, kunskapsnivå, matematik 2b
Innehållsförteckning
1 Förord ................................................................................................................................................... 4
2 Inledning............................................................................................................................................... 5
2.1 Bakgrund ....................................................................................................................................... 6
2.2 Syfte och frågeställningar .............................................................................................................. 7
3 Teoretiska utgångspunkter ................................................................................................................... 8
3.1 Kunskapsnivåer inom geometri ..................................................................................................... 8
3.2 Matematiska kompetenser ............................................................................................................. 8
4 Metod ................................................................................................................................................. 11
4.1 Val av undersökningsmetod ........................................................................................................ 11
4.2 Konstruktion av kunskapstest ...................................................................................................... 11
4.3 Studiens genomförande ............................................................................................................... 12
4.4 Presentation av kunskapstestet .................................................................................................... 13
4.5 Analys av elevuppgifter............................................................................................................... 18
5 Resultat ............................................................................................................................................... 18
5.1 Matematiska kompetenser ........................................................................................................... 18
5.1.1 Begreppskompetens.............................................................................................................. 18
5.1.3 Problemlösningskompetens .................................................................................................. 20
5.1.4 Modelleringskompetens ....................................................................................................... 21
5.1.5 Kommunikationskompetens ................................................................................................. 23
5.1.6 Resonemangskompetens....................................................................................................... 24
5.2 Geometriska kunskapsnivåer enligt van Hiele ............................................................................ 24
5.3 Sammanfattning av det totala resultatet ...................................................................................... 26
6 Diskussion .......................................................................................................................................... 28
6.1 Matematiska kompetenser ........................................................................................................... 28
6.2 Matematiska kunskapsnivåer enligt van Hiele ............................................................................ 29
6.4 Slutkommentarer och implikationer för undervisning................................................................. 30
7 Referenser........................................................................................................................................... 31
Bilaga 1. Kunskapstest .......................................................................................................................... 33
Bilaga 2. Skolverkets korrekta lösningar av uppgift 1, 2, 3 och 5......................................................... 35
Bilaga 3. Lösningsförslag till testet ....................................................................................................... 36
Bilaga 4. De grundläggande klassiska satserna inom geometri............................................................. 38
1 Förord
Geometri är det område som enligt min erfarenhet av fem år som matematiklärare i Vietnam
upplever som det område inom matematik där eleverna presterar resultatmässigt lägst. Jag
upplever att detsamma gäller för Sverige efter att ha jobbat som extralärare och praktiserat
under min VFU (verksamhetsförlagda utbildning). Detta gör att jag blir nyfiken på att ta reda
på varför det är så och jag har bestämt mig för att ta reda på mer om geometriområdet. Att
skriva examensarbetet om geometri ger mig möjlighet att förstå mer om elevers förståelse för
geometrin, samt det ger också mig möjligheten att utveckla min egen undervisning i geometri.
Min egen eleverfarenhet av geometri är att jag upplevde geometrin som lätt. Det intresserade
mig och var mitt mest älskade område inom matematik. Mitt minne från den första
geometrilektionen är ifrån högstadiet och det var tråkigt när läraren gav en introduktion om
begrepp med till exempel: punkter, linjer, plan, sträckor, vinklar, trianglar mm. Sedan blev det
mycket mera intressant när läraren hade en genomgång om kongruens. Den lektionen öppnande
en dörr för mig och där kom jag att bli intresserad av matematik. Innan dess var jag en elev som
inte kunde matematik men efter det var jag som en annan elev. Anledningen till att jag
uppskattade geometrin i matematik på den lektionen var att läraren lät alla elever bli delaktiga
och fick visa färdigheter och kunskaper i lärarens samtal med klassen. Det som var särskilt
speciellt på lektionen var att han pekade ut tankegångarna vid problemlösning men också hur
man skulle redovisa uppgifter i skriftligt. Eftersom det här sättet fungerade för mig som elev
använde jag samma sätt som min gamla lärare på geometrilektionerna när jag själv arbetade
som lärare men resultatet blev inte som förväntat. Med denna studie hoppas jag kunna hitta ett
bättre fungerande sätt att undervisa geometri för eleverna.
4
2 Inledning
Resultaten från de nationella kursproven i Matematik 2b mellan våren 2013 till våren 2015 visar
på att många elever inte klarar betyget E. På kursprovet godkändes knappt 40% av eleverna och
drygt 25% fick icke godkända kursbetyg (medelvärden över tid; tabell 1). Med det här resultatet
växer behovet hos oss matematiklärare att ta reda på orsaken till att eleverna inte klarar proven.
Tabell 1. Icke godkända provbetyg och kursbetyg i matematik 2b från våren 2013 till våren
2015. Data i tabell 1 är hämtade från Skolverket (2013; 2014a; 2014b; 2015a; 2015b).
Vt 13
Ht 13
Vt 14
Ht 14
Vt 15
Medelvärde
28,4 %
39,4 %
40,4 %
37,8 %
51,3 %
39,46 %
15,2 %
39,5 %
23,4 %
25,0 %
25,7 %
25,76 %
Icke
godkända
nationella
prov
Icke
godkända
kursbetyg
5
2.1 Bakgrund
Historiskt sett utvecklades geometri med samhällets behov av att uppföra större byggnader,
staka ut land, bygga bevattningsanläggningar, göra astronomiska observationer etc. Då behövde
människor kunskaper i geometri för att beräkna areor, volymer och vinklar. Euklides gjorde en
”revolution” i geometri genom den axiomatiska metoden (Lindahl, 2004). Den geometri som
elever läser i skolan har ett underlag i euklidisk geometri. Utgående från grundläggande begrepp
som punkt, sträcka, linje och cirkel formulerade Euklides följande fem geometriska postulat
och fem allmänna axiom:
De fem postulaten är:
”1. Man kan dra en (unik) sträcka mellan varje par av punkter.
2. Varje sträcka kan (på ett unikt sätt) förlängas till en linje.
3. Man kan beskriva en cirkel med godtycklig medelpunkt och godtycklig radie.
4. Alla räta vinklar är lika.
5. Om en linje skär två linjer så att summan av två inrevinklar på samma sida om den skärande
linjen är mindre än två räta vinklar, så skär de två linjerna varandra på den sida där de båda
vinklarna ligger”. (Lindahl, 2004, s. 8)
De fem allmänna axiomen är:
”1. Storheter som är lika med en och samma storhet är också inbördes lika.
2. Om lika storheter adderas till lika storheter så är summorna lika.
3. Om lika storheter subtraheras från lika storheter så är skillnaderna lika
4. Storheter som sammanfaller med varandra är lika.
5. Det hela är större än sina delar.
Storheter syftar i Elementa på t ex sträckor, vinklar och trianglar, och likhet används bl a i
betydelsen kongruens”. (Lindahl, 2004, s. 8)
Kursen Matematik 2b i gymnasieläroplanen 2011 har 15 punkter med centralt innehåll, där
varje punkt kan innehålla många delmoment. De 15 punkterna delas in fyra stora områden. Den
första består av Taluppfattning, aritmetik och algebra. Den andra av Geometri. Den tredje av
Samband och förändring. Den fjärde och sista består av Sannolikhet och statistik.
Geometridelen står som en egen punkt där man ska belysa ”Användning av grundläggande
klassiska satser i geometri om likformighet, kongruens och vinklar” (Skolverket, 2011a, s. 110).
6
Den här punkten beskrivs inte så tydligt i kunskapskraven. Där beskriver Skolverket (2011a, s.
111) bara generella ordalag som till exempel ”eleven kan formulera, analysera och lösa
matematiska problem”. Det finns ingen tydlig riktlinje som lärarna skall följa och arbeta med
inom geometriområdet och då blir det är upp till läraren att tolka hur undervisningen ska ske.
Det finns inte heller några kommentarer för vilka förmågor eleven behöver träna på inom
geometrin. De förmågor elever behöver utveckla i geometrin ligger under samtliga
matematikkurser. Detta medför att geometriområdet kan bli brett eller smalt i centrala
innehållet beroende på hur lärarna tolkar det.
2.2 Syfte och frågeställningar
Studiens begränsning i det här examensarbetet är att undersöka geometri i matematik 2b i
läroplanen 2011. Jag presenterar van Hieles teori om kunskapsnivåer och de sex matematiska
kompetenserna enligt Palm, Bergqvist, Eriksson, Hellström & Häggström (2004), och
använder dessa verktyg för att bedöma elevernas kunskapsnivåer och kompetenser i geometri.
Studiens syfte är att få en uppfattning om gymnasieelevers kunskap om avsnittet geometri i
kursen Matematik 2b. Detta leder till följande forskningsfrågor:

I vilken utsträckning har gymnasieelever de sex matematiska kompetenserna i
geometriavsnittet i kursen Matematik 2b?

Vilken kunskapsnivå i geometri enligt Van Hieles klassificering uppnår
gymnasieelever?
7
3 Teoretiska utgångspunkter
3.1 Kunskapsnivåer inom geometri
I boken Geometri och statistik presenterar Hedrén (2007) van Hieles fem kunskapsnivåer i
geometri (van Hiele, 1986). Denna teori som kan användas för att förstå elevens utveckling
inom geometrin. Teorin bygger på fem olika nivåer:
”Nivå 1. Igenkänning (Visualisering). Eleven lär sig vissa termer och känner igen
en geometrisk figur som en helhet. Eleven tar ingen hänsyn till figurens delar. En
elev på denna nivå kan till exempel känna igen en bild av en rektangel men är i
allmänhet inte medveten om några egenskaper hos rektangeln, som t ex att den har
parallella sidor. Eleven liknar gärna rektangeln med t ex en dörr eller en fönsterruta.
Nivå 2. Analys. Eleven kan analysera egenskaper hos figurer empiriskt genom att
vika papper, mäta, rita på rutat papper eller använda geobräde. På denna nivå kan
eleven inse att motstående sidor hos en rektangel är parallella och kongruenta men
hon kan ännu inte se sambandet mellan rektanglar eller kvadrater och rätvinkliga
trianglar. Hon vet inte heller att en kvadrat kan ses som en rektangel eller som en
romb.
Nivå 3. Abstraktion. Eleven kan logiskt ordna figurer, t ex alla kvadrater är
rektanglar, men alla rektanglar är inte kvadrater. Hon förstår de inbördes sambanden
mellan figurer och inser vikten av korrekta definitioner. Även om hon förstår
sambandet mellan mängden av kvadrater och mängden av rektanglar samt mellan
mängden av rektanglar och mängden av parallellogrammer, kan hon inte härleda
varför t.ex. diagonalerna i rektangel är kongruenta. Hon förstår inte deduktionen roll
i geometrin.
Nivå 4. Deduktion. Eleven förstår betydelsen av deduktion och den roll axiom, satser
och bevis spelar i geometrin. På denna nivå kan eleven använda axiom för att bevisa
påståenden om t ex rektanglar och trianglar, men hennes tänkande är i allmänhet
inte så precist att hon förstår nödvändigheten av axiom.
Nivå 5. Stringens. Eleven förstår vikten av precision, när man arbetar med
geometrins grunder, som t ex Hilberts axiomsystem för geometrin. Hon kan utveckla
en teori utan användning av konkreta föremål. Hon kan t ex också analysera och
jämföra euklidisk och icke-euklidisk geometri”. (Emanuelsson, Johansson &
Ryding, 2007, s. 28).
3.2 Matematiska kompetenser
Ordet kompetens är synonymt med kunnighet och skicklighet. Kompetens kopplar till en
kombination av olika slags kunskaper och färdigheter som sätter en person i stånd att göra
något. Kompetens handlar då om vad en person vet och kan göra inom ett ämnesområde, oavsett
hur eller när dessa kunskaper eller färdigheter har förvärvats (Korp, 2011).
Ordet förmåga ses som något som inte påverkas av undervisning eller är kopplat till
kunskapsutveckling. Man kan t.ex. tala om kognitiv förmåga eller empatisk förmåga som i
första hand är psykologiska begrepp. Men ordet förmåga kan också ses som kapacitet att göra
något, exempelvis att bedöma elevers läsförmåga med hjälp av ett utprovat test handlar då om
att bedöma var i sin läsutveckling som olika elever befinner sig och därmed vad de behöver
8
bäst för att komma vidare. Testningen blir då något som lärare kan göra för att på bästa sätt
kunna anpassa undervisningen efter elevernas resurser och behov (Korp, 2011).
I ämnesplanens syfte för matematik anges sju matematiska förmågor som elever behöver
utvecklas för att arbeta med matematik. De sju matematiska förmågorna är begreppsförmåga,
procedurförmåga, problemlösningsförmåga, modelleringsförmåga, resonemangsförmåga,
kommunikationsförmåga och relevansförmåga (Skolverket, 2011a & 2011c). Några av de sju
matematiska förmågorna beskrivs inte så tydligt och det finns inte några exempel, exempelvis
beskriver Skolverket kommunikationsförmåga som: ”... kommunicera matematiska
tankegångar muntligt, skriftligt och i handling” (Skolverket, 2011a, s. 91). I kommentarer till
ämnet förtydligas förmågan på detta sätt: ”Kommunikationsförmåga är inte bara att kunna
kommunicera med hjälp av termer, symboler, tabeller, grafer utan även med hjälp av ord,
bilder, ritningar, gestaltningar och modeller och att anpassa sin kommunikation till
sammanhanget.”
(Skolverket,
2011c,
s.
3).
Enligt
Skolverket
(2011a)
handlar
relevansförmågan om att synliggöra var matematiken finns såväl i vardagen som i
programinriktningarnas olika karaktärer. Skolverket (2012a) belyser att i de nationella proven
testas inte förmågans relevans utan detta överlåts till den undervisande läraren.
Palm, Bergqvist, Eriksson, Hellström och Häggström (2004) har presenterat sex matematiska
kompetenser som man kan använda för att bedöma elevers kompetenser i matematik. Jag tycker
att de sex matematiska kompetenserna är ett väl förklarat och begrepp är entydiga. I sin rapport
har Palm m.fl. också presenterat många olika uppgifter som författarna plockar ur från olika
nationella prov från hösten 1995 till våren 2002, där har Palm m.fl. förklarat mycket tydligt att
vilka uppgifter som tillhör respektive kompetens. Detta tillsammans med definitioner av två
begrepp kompetens och förmågor ovanför är anledningar att i den här studien använder jag de
sex matematiska kompetenser som beskriver av Palm m.fl. Nedanstående tabell visar
sambandet mellan förmågor oh kompetenser:
Förmåga
Kompetens
Begreppsförmåga
Begreppskompetens
Procedurförmåga
Algoritmkompetens
Problemlösningsförmåga
Problemlösningskompetens
Modelleringsförmåga
Modelleringskompetens
Resonemangsförmåga
Resonemangskompetens
Kommunikationsförmåga
Kommunikationskompetens
9
Nedanför citateras beskrivningar av de sex kompetenserna.
Problemlösningskompetens
”Med problemlösningskompetens menas att kunna lösa det vi här kallar problem, d v s
uppgifter där uppgiftslösaren inte har någon färdig lösningsmetod tillgänglig. Eleven
behöver producera någon form av (icke rutinmässig) kunskap, d v s tillämpa sina kunskaper
på en för honom eller henne ny situation. Huruvida en uppgift kräver
problemlösningskompetens för sin lösning beror då inte bara på egenskaper hos uppgiften
utan är beroende på kombinationen uppgift och uppgiftslösare” (Palm et al. 2004, s. 9).
Algoritmkompetens
”Med algoritmkompetens menas att känna till och kunna använda för kursen relevanta
algoritmer. Med detta menas att känna till och vid uppgiftslösning rutinmässigt kunna
använda procedurer i ett eller flera steg där alla stegen och den övergripande ordningsföljden
för de ingående stegen är väl kända för uppgiftslösaren. Varje steg i proceduren kan i sin tur
ofta beskrivas som en sekvens av mera elementära steg” (Palm et al. 2004, s. 12).
Begreppskompetens
”Med begreppskompetens menar vi en förtrogenhet med innebörden av ett begrepps
definition. Detta inkluderar förmågan att definiera och använda innebörden av ett begrepp.
För att få en tydlig bild av en elevs begreppskompetens när det gäller ett visst begrepp så är
det nödvändigt att använda ett flertal uppgifter med olika infallsvinklar. En elevs lösningar
till enstaka uppgifter kan dock indikera, mer eller mindre väl, elevens begreppskompetens”
(Palm et al. 2004, s. 13).
Modelleringskompetens
”Modelleringskompetens innefattar att utifrån utommatematiska situationer skapa och
använda en matematisk modell, tolka de resultat som den matematiska modellen ger när den
används samt utvärdera den matematiska modellen genom att klargöra dess begränsningar
och förutsättningar” (Palm et al. 2004, s. 17).
Resonemangskompetens
”Med resonemang avses här en argumentering som sker på allmänna logiska och speciella
ämnesteoretiska grunder. Det inkluderar deduktiva resonemang där logiska slutledningar
görs baserade på specifika antaganden och regler, där den striktaste formen av resonemang
kan sägas vara bevis. Det inkluderar också induktiva resonemang där allmänna slutsatser nås
fram till genom resonemang baserade på enskilda iakttagelser av mönster och
regelbundenheter. Det innebär att det i resonemangskompetensen ingår en undersökande
verksamhet av att hitta mönster, formulera, förbättra och undersöka hypoteser. Det
inkluderar också olika former av kritisk granskning, som t ex värdering av bevis och andra
former av matematiska argument. Resonemang ska kunna föras dels som en algoritmisk
aktivitet med redan kända argument och bevis och dels som en problemlösande aktivitet i
nya situationer” (Palm et al. 2004, s. 25).
Kommunikationskompetens
”Med kommunikationskompetens avser vi här förmågan att kunna kommunicera om
matematiska idéer och tankegångar såväl i muntlig som i skriftlig form. Detta innebär att
kunna ta emot och förstå information med matematiskt innehåll och också att kunna
producera och förmedla sådan information. Det betyder bland annat att förstå matematisk
terminologi och matematiska begrepp och att kunna använda dessa på lämpligt sätt i en
flervägskommunikation” (Palm et al. 2004, s. 30).
10
4 Metod
4.1 Val av undersökningsmetod
Analysmetoden som använts i studien är kvalitativ innehållsanalys. Innehållsanalys är ett
angreppssätt vid analys av dokument och texter och som på ett systematiskt sätt syftar till att
kvantifiera innehållet utifrån kategorier som bestämts i förväg (Bryman, 2011). En kvalitativ
innehållsanalys innebär att man söker efter bakomliggande teman och innebörder i
textmaterialet (Bryman, 2011).
För att besvara forskningsfrågorna har jag konstruerat ett kunskapstest. Fyra av uppgifterna har
valts ut från de nationella proven för matematik kurs2b. De fyra nationella provuppgifterna
valdes för att uppgifterna skall vara relevanta och autentiska. I kunskapstestet ingår ytterligare
en egenkonstruerad uppgift. Uppgiften har sitt ursprung i boken Origo (Szabo, Larson, Viklund,
Dufåker och Marklund, 2012, uppgift 5246) och har valts för att den användes i undervisningen
på den för studien aktuella gymnasieskolan. Med teoretiska utgångspunkter i kompetenser och
kunskapsnivåer har jag använt innehållsanalys för att tolka mitt material.
Denna studie är en pilotstudie, som kan följas av en större studie av flera klasser med flera
personer som kodar proven. Fördelen med detta är att skapa en helhet bild av elevers kunskap,
dvs detta ska underlätta att identifiera attityder. Vilket är ett verktyg för lärarna att orientera
och justera undervisningen på ett effektivt och lämpligt sätt med läroplanen.
4.2 Konstruktion av kunskapstest
För att studera eleverna kunskaper inom geometri har ett kunskapstest konstruerats och använts
(se Bilaga 1). Kunskapstestet består av fem uppgifter varav fyra av de fem uppgifterna
(uppgifterna 1, 2, 3 och 5) härstammar ifrån fyra olika nationella prov i matematikkurs 2b och
matematikkurs B. Matematikkurs B motsvarar matematikkurs 2a, 2b eller 2c. Det är därför de
uppgifterna väljs från matematikkurs B med syfte att vara lämpligt med matematikkurs 2b.
Syftet med kunskapstestet var att testa geometrikunskaper för att bedöma elevernas
kunskapsnivåer och dess kompetenser inom geometridelen av kursen Matematik 2b. Av tabell
2 framgår vilken uppgift som behandlar vilka kompetenser och kunskapsnivåer enligt van
Hiele.
11
Tabell 2. Fördelning av uppgifter angivet kompetenser och kunskapsnivåer.
Uppgift
Kompetenser
Kunskapsnivåer
1
Begreppskompetens, Algoritmskompetens
1, 2
2
Begreppskompetens, Problemlösningskompetens
2, 3
3
Algoritmskompetens, Resonemangskompetens
1, 2, 3
4
Resonemangskompetens, Kommunikationskompetens
2, 3, 4
5
Modelleringskompetens
2, 3, 4
Uppgifterna i de nationella proven är utprövade i klasser av Skolverket. Eftersom
kommunikationskompetens inte prövades i uppgifterna 1,2,3 och 5, tillkom en egenkonstruerad
uppgift (4), vilkens syfte var att testa just den skriftliga kommunikationskompetensen.
Uppgiften är en version av uppgift 5246 i boken Matematik Origo 2b (Szabo m.fl., 2012, s.
184), och också är med i lärarens utdelade lektionsplanering. Min version har inte använts i
någon klass, vilket öppnar för missuppfattningar av uppgiften.
4.3 Studiens genomförande
Undersökningen har genomförts på en svensk gymnasieskola. Eleverna tillhör två olika klasser
och studerar det samhällsvetenskapliga programmet med inriktningen beteendevetenskap.
Anledning till att jag valde de här klasserna är för att min VFU handledare undervisade i dessa
klasser och det var min enda kontakt in i den svenska skolan. Totalt deltog 47 elever. Alla elever
studerar kursen matematik 2b och har samma undervisande lärare, som använder sig av samma
bok, Matematik Origo 2b, (Szabo m.fl., 2012) för de båda klasserna. Det betyder att eleverna
som deltar går samma matematikkurs, går samma gymnasieprogram, har samma bok och
undervisas av samma lärare.
Eleverna fick självständigt svara på det tidigare nämnda kunskapstestet och hade ungefär 50
minuter till förfogande. Elevernas arbetsmaterial och hjälpmedel var penna, sudd och
mobiltelefoner som miniräknare. Läraren som undervisar i klasserna delade ut det skriftliga
kunskapstestet till eleverna och vaktade klasserna. Eleverna hade läst avsnittet Geometri i
kursen matematik 2b i december 2015 men kunskapstestet utfördes i mars 2016.
I min studie har jag tagit hänsyn till de fyra etiska principer som utgivits av Vetenskapsrådet
(2002). Den första principen, informationskravet innebär att man ska informera om syftet med
undersökning. I denna studie informerade jag deltagarna två veckor innan kunskapstestet
12
genomfördes. Den andra principen, samtyckeskravet innebär att deltagare själva får bestämmer
om de vill vara med eller inte. Detta krav uppfylldes då deltagare i den här undersökningen är
över 15 år och det var frivilligt att deltaga i kunskapstestet. Av totalt 54 elever i två klasser
valde 7 elever, av olika anledningar, att inte deltaga i kunskapstestet. Den tredje principen är
konfidentialitetskravet. I min undersökning är deltagarna anonyma; namnen är fiktiva. Den
fjärde principen är nyttjandekravet och materialet jag samlade in i den här undersökningen
hanterades så att ingen obehörig kunde komma åt det. Det användes endast för denna studie och
raderades sedan studien hade slutförts.
4.4 Presentation av kunskapstestet
Uppgift 1. (Skolverket, 2005, uppgift 3)
a)
Bestäm vinkeln x
b)
Vilket eller vilka av följande geometriska samband använde
du då du bestämde vinkeln x?
Endast svar fordras
A. Pythagoras sats
B. Vinkelsumman i en triangel är 180°
C. Summan av sidovinklar är 180°
D. Yttervinkelsatsen
E. Topptriangelsatsen
F. Randvinkelsatsen
Uppgift 1 testar om eleverna klarar av att beräkna vinklar. I deluppgift 1a skall eleven använda
sig av kända geometriska samband mellan vinklar som yttervinkelsatsen eller kombination av
vinkelsumman i en triangel och summan av sidovinklar. Det senare innebär att eleven kan
genomföra varje delsteg i proceduren för att komma fram till lösningen. Detta innebär att
deluppgift 1a testar om algoritmkompetens. I deluppgift 1b testas om eleven kommer ihåg vilka
kunskap som används eller eleven räknar på ett mekaniskt sätt. Detta betyder att deluppgift 1b
testar begreppskompetens.
Uppgift 1 skall visa om eleven befinner sig på nivå 1 eller 2.
13
Tabell 3. Lösningar innehåller detaljer som exemplifierar van Hiele nivåerna 1 - 2.
Nivå
1
2
Lösning Räkna från utseende t.ex. elever Summan av sidovinklar är 1800 .
kan gissa att en vinkel av
Vinkelsumman i en triangel är 1800 .
triangel är 300 eller elever kan
En yttervinkel till en triangel är lika med
gissa att triangeln är likbent.
summan av de två motstående inre
Eleven kan inte skilja mellan en
vinklarna.
likbent triangel och en ”vanlig”
triangel.
Uppgift 2. (Skolverket, 2012b, uppgift 16)
Två likformiga rektanglar har olika mått. Rektangel A har sidorna 4 cm och 6 cm.
Rektangel B har en sida som är 12 cm.
Vilka mått kan den andra sidan hos rektangel B ha?
Uppgift 2 behandlar likformighet. I lösningen av denna uppgift ingår att eleven förstår
innebörden (likformighetsskalan) av begreppet likformighet och använder begreppet i olika
situationer. För att komma fram till korrekt lösning måste eleven förstå att två fall är möjliga.
Enligt Skolverket (2012b) skall uppgiften testa elevers förmågor inom begreppskompetens och
problemlösningskompetens på E-nivå.
Uppgift 2 skall visa om eleven befinner sig på nivå 2 eller 3.
Tabell 4. Lösningar innehåller detaljer som exemplifierar van Hiele nivåerna 2- 3.
Nivå
2
3
Lösning Likformighetsskalan
Likformighetsskalan
Resonera om rektangels relationer i
olika sammanhang och konstruera
rektangels sidor
14
Uppgift 3. (Skolverket, 2002, uppgift 7)
Punkterna A, B och C ligger på en cirkel.
O är cirkelns medelpunkt. Bestäm vinklarna i triangeln ABC.
Mätning i figur accepteras ej
Uppgift 3 testar om eleverna klarar av att beräkna vinklar i svåra relationer, där det krävs att
eleven kan skapa resonemangskedjor. I uppgiften skall eleven använda sig av kända
geometriska samband mellan vinklar som randvinkelsatsen, vinkelsumman i en triangel och
relationen mellan vinklar i en likbent triangel. Att skapa resonemangskedjor innebär att
genomföra varje steg i proceduren och att logiskt med användning av relevanta satser finna
lösningen.
Detta
innebär
att
uppgift
3
testar
om
algoritmkompetens
och
resonemangskompetens.
Uppgift 3 skall visa om eleven befinner sig på nivå 1,2 eller 3.
Tabell 5. Lösningar innehåller detaljer som exemplifierar van Hiele nivåerna 1 - 3.
Nivå
1
Lösning Räkna från utseende
2
3
Randvinkelsatsen.
Randvinkelsatsen.
t.ex. elever kan gissa
Vinkelsumman i en
Vinkelsumman i en
att vinkeln ABO och
triangel är 1800 .
triangel är 1800 .
vinkeln CBO är lika
Basvinklarna i en
Basvinklarna i en
stora eller elever kan
likbent triangel är lika
likbent triangel är lika
gissa att triangeln
stora.
stora.
ABC är likbent.
Förstå relationen
Eleven kan inte skilja
mellan figurens vinklar
på en likbent och en
oh kunna räkna på ett
”vanlig” triangel.
korrekt sätt.
15
Uppgift 4.
A
I den likbenta triangeln ABC är basen BC. Punkt M är mittpunkt på BC.
Förklara att trianglarna ABM och ACM är kongruenta.
B
M
C
Uppgift 4 behandlar kongruens. I denna uppgift ska eleverna förklara egenskaperna hos en
likbent triangel och mittpunkt på en sträcka och därigenom kunna bevisa påståendet genom att
använda ett av de tre kongruensfallen. Uppgift 4 testar resonemangskompetens och
kommunikationskompetens i skrift.
Uppgift 4 skall visa om eleven befinner sig på nivå 2,3 eller 4.
Tabell 6. Lösningar innehåller detaljer som exemplifierar van Hiele nivåerna 2 - 4.
Nivå
2
3
Lösning Två sidor är lika långa i Två sidor är lika långa i
4
Använd en av tre
en likbent triangel.
en likbent triangel.
kongruensfall för att
Mittpunkten av en
Mittpunkten av en
förklara på ett korrekt
sträcka delar sträckan i
sträcka delar sträckan i
sätt.
två lika långa delar.
två lika långa delar.
Eleven kan inte se
Använd ett ”fel”
sambandet mellan
kongruensfall, där har
given och tre
eleven missförstånd
kongruensfall.
med tre kongruensfall
som t ex. använd ”sidasida-vinkel” eller
”vinkel-vinkel-sida”.
16
Uppgift 5. (Skolverket, 2011b, uppgift 11)
Lina och Sara är ute och seglar i en båt som de har lånat. De seglar mot en bro och
börjar fundera på om masten är för hög för att båten ska kunna passera under bron.
För att kunna bestämma mastens höjd gör de några mätningar.
Lina och Sara mäter avståndet från mastens fot och rakt ut mot akterstaget och finner
att det är 4,50 m. Sedan mäter de avståndet från masten till akterstaget 0,80 m högre
upp och parallellt med första mätningen. Det avståndet är 4,20 m. Se figur.
Använd de mätningar som Lina och Sara har gjort och bestäm mastens höjd.
Uppgift 5 behandlar likformighet. Uppgiften handlar om en situation ur verkligheten utanför
skolan. För att komma fram till lösningen skall elever kunna formulera en geometrisk
beskrivning utifrån en realistisk situation. Enligt Skolverket (2011b) skall uppgiften testa
elevers förmågor inom modelleringskompetens.
Uppgift 5 skall visa om eleven befinner sig på nivå 2,3 eller 4.
Tabell 7. Lösningar innehåller detaljer som exemplifierar van Hiele nivåerna 2 - 4.
Nivå
2
Lösning Likformighetsskalan
3
4
Formulering.
Formulering.
Topptriangelsatsen.
Topptriangelsatsen.
Koppla till praktiken
för att svara.
17
4.5 Analys av elevuppgifter
De skriftliga lösningarna samlades in och analyserades separat för varje uppgift både med
avseende på kompetenser och van Hiele nivåer. De skriftliga kunskapstesterna bedömdes och
analyserades enligt Palm et al. (2004) kompetenser och van Hiele nivåer. I bilaga 2 redovisas
Skolverkets bedömningsmallar för uppgifterna 1,2,3 och 5. Bilaga 3 har skapats av mig, och
det är ett förslag på korrekta lösningar till uppgifterna, och elevsvaren har jämförts med dessa.
Bilaga 4 ger en sammanfattning av relevanta satser i geometri och användes för att bestämma
elevlösningarnas van Hiele nivåer.
5 Resultat
Resultatet är uppdelat i tre delar. Den första delen ger resultatet av analysen av elevlösningarna
med avseende på visade matematiska kompetenser och den andra med avseende på visade van
Hiele nivåer. I den tredje delen ges en sammanfattning.
5.1 Matematiska kompetenser
5.1.1 Begreppskompetens
Begreppskompetens testas, som tidigare nämnt, i deluppgift 1b och uppgift 2 i kunskapstestet.
I deluppgift 1b hade 25 av 47 elever fel svar. Huvudorsaken var att de inte kunde skilja på
summan av sidovinklar och yttervinkelsatsen. De var alltså osäkra på begreppens innebörd,
vilket tyder på brister i deras begreppskompetens.
På den andra begreppsuppgiften (uppgift 2) har 27 elever förstått begreppet och har använt
likformighetsskalan för att finna en eller två lösningar. Nedan redovisas lösningar av två elever,
som båda har funnit endast ett av de två möjliga svaren.
”A har en lång sida på 6 cm och en kort sida på 4 cm.
Eftersom B och A är likformiga så dubbelt jag A:s sidor.
B:s sidor blir alltså 12 cm och 8 cm” (Linda-elev)
18
Eller ”
4
A
a
6
4
a
=
6
12
B
→ 12.
12
4
= a
6
48
= a
6
→8 = a
→
a=8
Svar:8 cm” (Emma-elev)
De här lösningarna är inte fullständiga men eleverna visar att de förstår begreppet likformighet,
vilket är det väsentliga i uppgiften.
Svaren på uppgift 2 visar också att 6 av 47 elever har lämnat blankt och åtta elever har motiverat
fel (tre av dessa elever ritat trianglar istället för rektanglar). Detta tyder på att dessa elever
antingen har missförstått uppgiftens text eller har brister i begreppskompetensen. Följande
lösning ger exempel på det senare:
”Rektangel A
Rektangel B
x
4 cm
6 cm
12 cm
6.4=24 cm2
Likformiga ska ha samma värde 12.x=24 cm2
x=2
Svar: 2 cm” (Solvej-elev)
Sex av eleverna har rätt svar utan motivering i uppgift 2. Enligt Skolverket (2012b) krävs det
en redovisning som leder fram till ett godtagbart svar för att få poängen. Detta tyder på att dessa
elever inte kan använda innebörden av begreppet, dvs deras begreppskompetens har brister.
19
5.1.2 Algoritmkompetens
Algoritmkompetens testas som tidigare nämnt, i deluppgift 1a och uppgift 3. Svaren på
deluppgift 1a visar att 45 elever kan använda enkla beräkningar i lösningen. De två elever med
felaktigt svar har gjort samma fel: ”1440 - 1800=360”. Deras förståelse av negativa tal har alltså
brister. Resultatet är alltså att 45 av eleverna kunde genomföra proceduren. De visade därmed
algoritmkompetens.
Svaren på uppgift 3 visar att 36 av de 47 elever, som hade räknat uppgiften, klarade att göra
beräkningar i flera steg. De hade kontroll på proceduren och visade därmed algoritmkompetens.
Ett elevexempel på lösning av uppgiften:
”Vinkel O=1400 är dubbelt så stor som
vinkel 𝐴 (i en cirkel är
medelpunktsvinkeln dubbelt så stor som
randvinkeln i samma cirkelbåge).
1400
A =
= 700
2
Vilket innebär att
.
Eftersom triangeln OCB är likbent är vinklarna C=B.
Triangelns vinkelsumma är 1800 i den ”lilla” triangeln.
1800 - 1400 = 400
400
= 200 = C = B
2
Vinkel A=700
Vinkel B=300+200=500
Vinkel C=1800-700-500=600” (Kelvin-elev)
5.1.3 Problemlösningskompetens
Problemlösningskompetens testas i flera uppgifter men i huvudsak i uppgift 2. För att få en
fullständig lösning på uppgiften ska eleverna kunna finna två fall. Elevsvaren på uppgift 2 visar
att 7 av 47 elever analyserar och tolkar uppgiften och finner de två möjliga svaren.
Nedan redovisas två använda metoder:
”Antingen är förhållandet mellan rektangel A och B en dubbelt
så stor alternativt tre gånger så stor.
20
4∙3=12 cm då är den andra 6∙3=18 cm
6∙2=12 cm då är den andra 4∙2=8 cm” (Anna-elev)
Eller
”Andra sidan hos triangeln = 𝑥
Alternativ 1: Antag att kortsidan är 12 cm och längsidan
x cm
4
6
=
12
x
12 cm
1
6
=
3
x
4 cm
6 cm
x
x=18
Svar: I så fall är sidan 18 cm
Alternativ 2: Antag att kortsidan är x cm och längsidan
12 cm
4
6
=
x
12
x
4 cm
6 cm
4
1
=
x
2
12 cm
x=8
Svar: I så fall är sidan 8 cm” (Johanna-elev)
Att endast 7 av 47 elever har löst uppgiften fullständigt visar att provdeltagarna i allmänhet har
stora brister i problemlösningskompetensen.
5.1.4 Modelleringskompetens
Modelleringskompetens testas i huvudsak i uppgift 5. Svaren på uppgift 5 visar att 39 elever
har lämnat blankt, 2 motiverat fel och 6 har löst uppgiften (ingen av 6 eleverna kommer fram
till korrekta lösningen). Detta visar på stora brister i modelleringskompetensen.
Sex elever som har visat beräkningar delas in i två modeller enligt följande exempel:
”Per 0,8 m blir seglet 30 cm smalare/ 0,3 m smalare.
När seglet är 0 cm brett är mastens topp.
4, 50 m är segelbreddens utgångspunkt
4,50m
= 15m
0,3m
21
Svar: Masten är 15 m hög.” (Johanna-elev)
Denna tankegång är på väg att bli rätt men eleven har svårt att skapa en matematisk modell
för att beskriva denna situation. Den matematiska modellen som står bakom elevens
redovisning är topptriangelsatsen (se uppgift 5 i bilaga 3).
Lösningen nedan visar att avståndet mellan skolans geometriundervisning och elevers förmåga
att översätta de geometriska satserna korrekt till ett modelleringsproblem är stort.
”
DE
CD
CE
=
=
AB
AC
BC
4,20
CD
=
4,50
CD + 0,8
4,20
(CD + 0,8)
= CD
4,50
4,20CD + 3,36
= CD
4,50
4,20CD + 3,36 = 4,50CD
3,36 = 4,50CD
4,20CD
11,2 = CD
Svar: 11,2 m” (Kelvin-elev)
Elevens lösning kan tolkas i två olika sätt. Första tolkningen är att eleven använder förhållandet
𝐷𝐸
𝐴𝐵
𝐶𝐷
= 𝐴𝐶 och sätter AD = 0,80 m trots att texten anger BE = 0,80 m, vilket tyder på att eleven
har bristande textförståelse. Andra tolkningen är att eleven använder förhållandet
4,20
𝐶𝐸
4,20
𝐷𝐸
𝐴𝐵
𝐶𝐸
= 𝐵𝐶. I
𝐶𝐷
stället för det korrekta nästa steget 4,20 = 𝐶𝐸+0,8 skriver eleven här 4,20 = 𝐶𝐷+0,8, vilket antyder
bristande kontroll mot texten. Samma bristande kontroll mot texten gör att eleven accepterar
svaret CD = 11,2 m, trots att längden av BC efterfrågas.
Detta visar att det finns stort avstånd mellan kunskap i skolan och användning av kunskap i
skolan i denna modelleringsuppgift.
22
5.1.5 Kommunikationskompetens
Kommunikationskompetens testas, som tidigare nämnts, i huvudsak i uppgift 4. Svaren på
uppgift 4 visar att 24 elever har lämnat blankt och bland annat har dessa elever skrivit: ”vet
ej vad kongruenta betyder” (Emilia-elev) och ”Ledsen Chau, jag har
ingen aning vad jag ska göra. Sorry bro…” (Axel-elev). Detta indikerar att
elever i den här gruppen inte förstår den matematiska terminologin och de matematiska
begreppen, alltså att eleverna har stora brister i begreppskompetens. Begreppskompetens är en
förutsättning för eleverna för att kunna visa kommunikationskompetens i skriftlig form.
Svaren på uppgift 4 visar också att tjugotvå elever har resonerat fel. Många elever av dessa
elever visar att inte heller de förstår matematisk terminologi eller de använder vardagsspråk att
kommunicera matematik. Ett elevexempel: ”Eftersom
triangeln
är
likbent
betyder det att en sida kan vara olik. Eftersom BA och CA är
lika långa betyder att BC är den sidan som inte är lik” (Marc-elev,
här använder han vardagsspråk istället för att använda matematiska ordet ”bas”), bland annat
har elever skrivit: ”De
är
bara
spegelvända” (Lin-elev), ”De
har
samma
storlek” (Björn-elev) eller påstått att ”Båda är lika stora” (Kenneth-elev) utan
förklaring. Dessa elever verkar visserligen förstå den geometriska situationen och kan redogöra
för den på ett vardagligt språk, men för att ha kommunikationskompetens måste man dessutom
i skrift kunna använda korrekta matematiska begrepp och korrekt matematisk terminologi.
Deras lösningar visar därför ingen kommunikationskompetens.
En av fyrtiosju elever har skrivit på uppgift 4 enligt följande:
”Alla motstående sidor ska vara lika långa.
A
Den är likbent ⇒ AB = AC (2 sidor lika långa)
B
M
C
Eftersom M är i
mellan BM och MC.
mitten blir längden lika
BM=CM
Sedan går M upp lika längd för båda trianglarna.
Alla sidor är alltså lika långa.” (Börje-elev)
Börjes redovisning kan tolkas med en kortfattade: ”AB=AC, BM=CM och AM är gemensam
sida, detta medför att ∆𝐴𝐵𝑀 ≅ ∆𝐴𝐶𝑀 (SSS)” (Se bilaga 3). Börjes förklaring är inte så tydligt
men det visar att eleven kan tolka och använda information och med matematisk terminologi
visa sin slutsats. Detta tyder på att eleven har kommunikationskompetens.
23
5.1.6 Resonemangskompetens
Resonemangskompetens testas, som tidigare nämnts, i uppgift 3 och uppgift 4. Svaren på
uppgift 3 visar att 5 av 47 elever beräknar vinklarna i triangeln ABC på ett godtagbart sätt. De
kan även utvärdera sina beräkningar och motivera dem med hänvisning till relevanta
geometrisatser och visar på så sätt resonemangskompetens (se exempel i avsnittet 4.1.2.
Algoritmkompetens).
Svaren på uppgift 4 visar att fyrtiosex elever inte kan resonera om uppgiften. Vissa elever vet
inte hur de ska börja, t ex. den elev som skrev ”jag har ingen aning vad jag ska
göra” (Axel-elev). Andra elever kan inte skilja mellan gissningar och välgrundade påstående,
t ex. de elever som skrev ”De är bara spegelvända” (Lin-elev), ”Triangeln är
delad på mitten, vilket gör dem kongruenta” (Angelica-elev) eller ”De
har samma storlek” (Viktor-elev). Några elever kan inte formulera korrekta bevis för
sina påståenden, t ex skriver Annika – elev ”Båda är lika stora” och Carina – elev
”Ja, dem är kongruenta” utan förklaring. Detta tyder på att elever saknar förmåga att
kunna göra, alltså på att deras resonemangskompetens har brister.
Svaren på uppgift 4 visar att 1 av 47 elever kan utföra en argumentering. Där använder eleven
kända begrepp som ”likbent triangel” och ”mittpunkt” för att komma fram att AB=AC och
BM=CM. Sedan använder eleven redan kända regler (kongruensfallet) för att basera på sitt
resonemang. Detta tyder på att eleven innehar resonemangskompetens.
5.2 Geometriska kunskapsnivåer enligt van Hiele
Lösningarna till deluppgift 1a visar vilka elever som befinner sig på nivå 1 och 2. Svaren på
deluppgift 1a visar att fyrtioen elever har analyserat egenskaper hos triangeln, det vill säga att
vinkelsumman i en triangel är 1800 eller att en yttervinkel till en triangel är lika med summan
av de motstående innervinklarna i denna uppgift. Ett elevexempel på lösning:
”Sidovinklar: 1440+y=1800
y=1800-1440=360
Triangelns vinkelsumma:360+1040+x=1800
x=1800-104-360=400” (Kelvin-elev)
24
Ett annat elevexempel:
”Enligt yttervinkelsatsen så ska x+1040=1440
Alltså x=1440-1040
x=400” (Kai-elev)
Sex elever som har svarat utan redovisning på separat papper har visat att de förstår egenskaper
hos triangeln genom att rita och skriva in i figuren på papperet. Exempel på elevlösning:
”
Svar:400” (Hampus-elev)
Detta visar att alla elever befinner sig på nivå 2 på denna uppgift.
Lösningen till uppgift 2 visar om eleven befinner sig på nivå 2 eller 3. Analys av elevernas svar
visar att 20 elever känner till egenskaperna hos likformighet och likformighetsskalan för att
jämföra två likformiga rektanglar. De bedöms därför befinna sig på nivå 2. 7 elever kan
resonera om rektangelns relationer i olika sammanhang (den sidan som är 12 cm ”ligger” eller
”står”) och de kan även konstruera rektangelns sidor. Dessa elever bedöms därför befinna sig
på nivå 3.
Lösningar till uppgift 3 ska kunna utvisa vilka elever som befinner sig på nivå 1, 2 och 3. Svaren
på uppgift 3 visar att arton elever hade motiverat fel och bedöms därför tillhöra nivå mellan 1
och 2 på grund av att å ena sidan känner de till att summan av tre vinklar i en triangel är 1800
alternativt medelpunktsvinkeln i en cirkel är 3600 , å andra sidan identifierar de figuren utifrån
deras utseende, till exempel påstår många elever att vinkeln ∧ 𝐴𝐵𝐶 är dubbelt så stor som
vinkeln ∧ 𝐴𝐵𝑂. Tio av eleverna har redovisat godtagbara beräkningar av en vinkel i triangeln
ABC. Dessa elever visar att de känner till och kan använda samband i figuren, till exempel
använder de sambandet mellan randvinkeln och medelpunktsvinkeln eller sambandet mellan
vinklarna i en likbent triangel för att beräkna. Detta tyder på att de tio eleverna tillhör nivå 2.
Åtta av de elever som klarat uppgiften har visat sina tankegångar i olika steg för att komma
25
fram till korrekt lösningen. Eleverna visar också att de förstår sambandet mellan vinklarna i
figuren. Vilket visar på att de åtta eleverna befinner sig på nivå 3.
Lösningar till uppgift 4 ska kunna utvisa vilka elever som befinner sig på nivå 2, 3 och 4. Svaren
på uppgift 4 visar att tjugotvå av fyrtiosju elever har resonerat fel. De här eleverna kan förklara
egenskap hos likbent triangel och mittpunkt på en sida men de vet inte hur man använder detta
för att bevisa påståenden, alternativt lösa problemet. Detta kan indikera på att elever i den här
gruppen tillhör nivå mellan 2 och 3. En av fyrtiosju elever kan logikens lagar, detta innebär att
eleven i uppgiften kan koppla givetvis information med ett kongruensfall på ett korrekt sätt för
att komma till lösningen. Vilket påpekar att eleven tillhör nivå 4.
Lösningen till uppgift 5 visar om eleven befinner sig på nivå 2, 3 eller 4. För att klara uppgiften
krävs både teoriförståelse och användning av teorin i en praktisk situation. Ingen av eleverna
gav en helt korrekt lösning och hade därför inte uppnått nivå 4. 4 av 47 elever använde
förhållandet mellan rektangelns sidor och bedömdes därför befinna sig på nivå 2. 2 av 47 elever
kunde formulera det matematiska problemet utifrån figuren och använda topptriangelsatsen för
att lösa det, dock var deras lösningar inte helt korrekta (se exemplet i avsnittet 4.1.4). Dessa 2
elever bedömdes befinna sig på nivå 3.
5.3 Sammanfattning av det totala resultatet
I detta avsnitt sammanfattas resultaten av undersökningen av kompetenser och van Hiele nivåer
i två tabeller.
Tabell 8. Kompetenser i geometri i matematik 2b.
Kompetens
Kommentarer av resultat
Brister i förståelse av begrepp:
53 % blandar ihop begreppen summan av
Begreppskompetens
sidovinklar och yttervinkelsatsen.
28 % har problem med begreppet likformighet.
6 % blandar ihop begreppen triangel och rektangel.
96 % klarar enklare beräkningar.
Algoritmkompetens
77 % klarar beräkningar i flera steg (algoritm).
26
85 % har problem med uppgiften som kräver mer än
Problemlösningskompetens
endast en användning av utantill inlärda regler,
uppgiften som krävs anlägga olika ansatser och
perspektiv.
Nästan 100 % har brister rimlighetsuppfattning i
Modelleringskompetens
Kommunikationskompetens
modelleringsuppgiften.
98 % har otillräcklig matematisk kommunikation
89 % kan inte använda informationen för att föra ett
Resonemangskompetens
resonemang algoritmisk med redan kända satser.
98 % har svårighet att konkretisera och föra
resonemang med hjälp av matematiska terminologi
och relevanta satser.
Tabell 8 visar att de flesta eleverna, som studerar kursen matematik 2b, har problem med
problemlösningskompetens,
modelleringskompetens,
kommunikationskompetens
och
resonemangskompetens. Många elever visar även brister i förståelse av olika matematiska
begrepp.
Tabell 9. Van Hiele nivåerna i geometri i matematik 2b. (De färgade rutorna visar vilka nivåer
som ingår i uppgiften, de ofärgade visar att ingen elev når den nivån).
Resultatet i tabell 9 visar att de flesta elever som studerar kursen matematik 2b befinner sig på
nivå 2 och 3.
Resultatet i två tabeller ovanför visar att eleverna behärskar algoritmkompetens och att en del
elever behärskar begreppskompetens. Resultatet visar också att de flesta av eleverna befinner
sig på kunskapsnivå 2 och 3. Många elever saknar således en djupare förståelse för geometrin
enligt analysen med kunskapsnivåer.
27
6 Diskussion
6.1 Matematiska kompetenser
Studiens ena syfte är att undersöka i vilken utsträckning elever behärskar de matematiska
kompetenserna inom geometrin. Resultatet av undersökningen visar att de flesta elever inte har
så stora problem när det gäller uppgifter med enklare beräkningar. Det visade sig att nästan alla
elever visade algoritmkompetens med hjälp av räknare. Enligt Palm et al. (2004) innebär det
att uppnå algoritmkompetens att elever bland annat behärskar hjälpmedel som exempelvis
miniräknare. Resultatet visar också att eleverna har algoritmkompetens. Enligt Edenström och
Selander (2013) är algoritmkompetens den kompetensen som tränas mest inom matematiken.
Pettersson (2008) hävdar att de flesta uppgifter i läroböcker och i prov är av algoritmisk
karaktär. Detta kan förklara till att eleverna har mer problem i andra kompetenser än
algoritmkompetens inom geometridelen.
Elevernas svårigheter som de möter i kunskapstestet är att motivera uppgifter, att analysera
egenskaper hos figurer och föra logiskt resonemang. Oförståelse av ett begrepps innebörd, syfte
och mening är en faktor som ger svårigheter, exempelvis har eleven skrivit ”vet ej vad
kongruenta betyder” (Olle-elev). Petterson (2008) konstaterar två anledningar till att elever har
problem med resonemang. För det första är att elever inte behärskar innebörden av begreppen.
För det andra saknar elever eller har för svaga uppfattningar om begreppen. Många elever i den
här studien har visat på brister i textförståelse och kompetenser när de inte vet hur man börjar
med uppgifterna. De har till exempel lämnat frågetecken och strecktecken efter frågor eller
skrivit ”jag har ingen aning vad jag ska göra” (Axel-elev). Detta kan vara att eleverna inte har
mött
uppgifterna
i
undervisningen
där
uppgifterna
handlar
om
att
använda
kommunikationskompetens och modelleringskompetens se till exempel uppgift 4 och uppgift
5.
Studien visar också att många elever har svårt att ta sig fram till ett korrekt svar. Det finns
många elever som endast kan klara av att beräkna en av vinklarna i triangeln ABC i uppgift 3.
Detta problem hade eleverna på grund av att de saknar förståelse av begrepp och satser. Detta
kan vara att eleverna under geometriundervisningen inte givits tillräckligt med möjligheter att
förstå de grundläggande geometriska satserna och den geometriska terminologin.
Eleverna har även svårt att skriva lösningar på ett tydligt sätt. De flesta elever skriver bara
beräkningar utan förklaring. Detta problem ingår inte i den här undersökningen men detta kan
tyda på att eleverna inte har så mycket möjligheter att träna på hur man skriva lösningar på ett
korrekt sätt eller hur man skriver resonemang i led till exempel a leder till b därför att… Vid
28
analysen är att förstå orsaken till att elever ger korrekta svar utan att motiverar dem. En
förklaring kan vara
att de inte har den behövliga kompetensen, en annan kan vara att
geometriundervisningen har ägnats åt mekanisk räkning utan krav på annat än svar.
6.2 Matematiska kunskapsnivåer enligt van Hiele
Studiens andra syfte var att undersöka vilken kunskapsnivå inom geometri elever kan uppnå
under kursen. Resultatet av undersökningen visar att det inte är så stor spridning på van Hiele
nivåerna på lösningarna; de flesta eleverna befinner sig på nivå 2 eller 3. Resultatet är förenligt
med van Hieles teori om att flertalet skolelever befinner sig på nivå 2,3 eller 4 (Storbacka,
2011). Storbacka (2011) belyser i sin förklaring av van Hieles teori också att de flesta elever är
på nivå 2 och 3, vissa elever kan uppnå nivå 4 men inga elever kan uppnå nivå 5.
Rutinuppgifter som uppgift 1 och 3 har eleverna inte större problem att lösa och nå upp nivåer
2 och 3. I uppgifter, som kräver utvärdering eller förklaringar, som uppgift 2 och 4, har eleverna
svårt att ta sig fram till korrekt svar och når inte upp till den högsta nivån som bedöms för
uppgiften. I uppgift 5 når få elever till nivåerna 2 och 3. Många elever har inte löst uppgifterna
2,3,4 och 5, varför deras nivå på dessa uppgifter inte kan bedömas.
6.3 Slutsats
Analysen visar att eleverna behärskar algoritmkompetens bäst av de matematiska
kompetenserna inom geometrin i matematik 2b. Algoritmkompetens är en viktig del av
geometriskt kunnande och bör inte tränas mindre men gärna kombineras med träning på de
andra kompetenserna för att ge eleverna bättre kunskaper i geometri.
För att förbättra andra kompetenser som resonemangskompetens, modelleringskompetens och
kommunikationskompetens hos elever, behöver lärare fokusera på begreppens definitioner på
genomgångarna.
Totalt sett är det ingen stor nivåspridning inom geometrin i kursen matematik 2b, om vi tittar
på nivåtillhörigheten på lösningar men om vi tittar på redovisningar kan vi se mycket större
variationer, t ex. i uppgift 1 några elever bara visar beräkningar. Där kan man inte skilja att
elever förstår rätt eller blandar av triangelns vinkelsumma med sidovinklar i deras tanke. Det
är svårt att utifrån bedömningar av en elevs nivå på enskilda problem göra en bedömning av
elevens sammanvägda nivå, eftersom nivån kan variera mellan uppgifterna.
Många elever i kursen matematik 2b saknar en djupare förståelse för geometrin enligt analysen
med van Hiele´s kunskapsnivåer.
29
Undersökningen har inte studerat geometriundervisningen men analysen av kursplanen har
visat att geometriområdet inte behandlas i undervisningen likvärdigt med andra område inom
matematik. Skolverket därför bör tydliggöra beskrivningen av geometridelen i kursplanemålen
eftersom analysen visar att eleverna inte behärskar många kompetenser inom geometrin.
6.4 Slutkommentarer och implikationer för undervisning
Det här arbetet har givit mig god förståelse om elevers kunskap i geometri, speciellt har jag fått
en tydlig bild av hur elever uppvisar olika kompetenser. Detta gör att jag i min kommande
lärarroll kan planera lektioner med en innehållsrik undervisning, som kan ge elever möjlighet
att fördjupa sina kunskaper och att visa sina kompetenser i geometri. Till exempel kan man
förbättra undervisningen i problemlösning och modellering. Begreppsbildning kan genomföras
på ett intresseväckande sätt genom att använda olika datorprogram med visualiseringar såsom
GeoGebra, Sketchpad, Desmos, med mera. Man kan också hjälpa eleverna att förstå att
matematiksproblem finns utanför skolan genom att träna på modelleringsuppgifter , som
behandlar problem i deras närhet. Ett
sätt att locka elevernas nyfikenhet i geometri är att man kan
börja lektion med en utmanade frågeställning, till exempel en modelleringsuppgift.
Att tolka elevers kunskapsnivåer i geometri med hjälp av van Hiele nivåer kan hjälpa mig att
avläsa eventuella missuppfattningar och förutse vilka fel eller problem elever kan har när de
löser uppgifter, så jag kan planera min undervisning bättre.
Några elever i undersökningen läser innantill utan att förstå innebörden av de matematiska
begreppen. Eleverna kan således inte förklara varför de gör som de gör. Många elever lämnade
även blankt i några uppgifter. Att intervjua elever för att förstå bakomliggande orsaker till att
elever inte kan förklara eller lämnade blankt skulle ge mig ytterligare information och en grund
för att variera undervisningen och därmed öka förståelsen hos eleverna.
Förslag på fortsatt forskning kan vara att göra en kvalitativ intervju. Det skulle också gå att göra
en undersökning genom att jämföra elevers kompetenser i geometri med deras kompetenser i
andra matematikområden. Ett intressant uppslag är också att undersöka eventuella samband
mellan elevers möjligheter att nå en viss van Hiele nivå i geometri och deras kompetenser.
30
7 Referenser
Bryman, Alan (2011). Samhällsvetenskapliga metoder (N. Björn, Övers.). (2. uppl.). Malmö:
Liber AB.
Edenström, C., & Selander, E. (2013). Matematikens sju förmågor. Några gymnasielärares
tolkningar och beskrivningar av sitt arbete med förmågorna (Examensarbete). Umeå: Umeås
universitet. Tillgänglig: http://umu.divaportal.org/smash/get/diva2:627696/FULLTEXT01.pdf
Hedrén, R. (2007). Van Hiele-nivåer och deras betydelse för geometriundervisningen. I
Emanuelsson G, Johansson B & Ryding R. (red). Geometri och statistik (s. 27 - 36). Lund:
Studentlitteratur.
Korp, H. (2011). Kunskapsbedömning: vad, hur och varför? Stockholm: Skolverket. Hämtat
från: http://www.skolverket.se/publikationer?id=2666 den 29 mars 2016.
Lindahl, Lars-Åke (2004). En inledning till geometri. Tillgänglig:
http://www2.math.uu.se/~lal/kompendier/Geometribok.pdf Hämtad den 24 mars 2016.
Palm, T., Eriksson, I., Bergqvist, E., Hellström, T. & Häggström, C. M. (2004). En tolkning
av målen med den svenska gymnasiematematiken och tolkningens konsekvenser för
uppgiftskonstruktion. Pm nr 199, Umeå: Umeå universitet.
Pettersson, K. (2008). Växelverkan mellan intuitiva idéer och formella resonemang. En
fallstudie av universitetsstudenters arbete med en analysuppgift. Nordic Studies in
Mathematics Education, 13 (1), 29–50.
Skolverket (2002). Nationellt kursprov i matematik kurs b våren 2002. Hämtat från:
http://www.edusci.umu.se/np/np-b-d/tidigare-prov/ den 20 mars 2016.
Skolverket (2005). Nationellt kursprov i matematik kurs b våren 2005. Hämtat från:
http://www.edusci.umu.se/np/np-b-d/tidigare-prov/ den 20 mars 2016.
Skolverket. (2011a). Läroplan, examensmål och gymnasiegemensamma ämnen för
gymnasieskola 2011. Stockholm: Skolverket.
Skolverket (2011b). Nationellt kursprov i matematik kurs b våren 2011. Hämtat från:
http://www.edusci.umu.se/np/np-b-d/tidigare-prov/ den 20 mars 2016.
Skolverket. (2011c). Ämne - Matematik. Hämtat från Skolverket med filens namn Alla
kommentarer: http://www.skolverket.se/laroplaner-amnen-ochkurser/gymnasieutbildning/gymnasieskola/mat?tos=gy&subjectCode=mat den 29 mars 2016.
Skolverket (2012a). Bedömningsexempel Matematik kurs 2b och 2c. Hämtat från
http://www.edusci.umu.se/np/np-2-4/exempel/ den 25 mars 2016.
Skolverket (2012b). Nationellt kursprov i matematik kurs b våren 2012. Hämtat från:
http://www.edusci.umu.se/np/np-2-4/tidigare-givna-prov/ den 20 mars 2016.
31
Skolverket (2013). Resultat från nationellt kursprov i Matematik 2abc, våren 2013, samt
lärarenkät. Hämtat från: http://www.edusci.umu.se/np/np-2-4/resultat/ den 25 mars 2016.
Skolverket (2014a). Resultat från nationellt kursprov i Matematik 2abc, hösten 2013, samt
lärarenkät. Hämtat från: http://www.edusci.umu.se/np/np-2-4/resultat/ den 25 mars 2016.
Skolverket (2014b). Resultat från nationellt kursprov i Matematik 2abc, våren 2014, samt
lärarenkät. Hämtat från: http://www.edusci.umu.se/np/np-2-4/resultat/ den 25 mars 2016.
Skolverket (2015a). Resultat från nationellt kursprov i Matematik 2abc, hösten 2014, samt
lärarenkät. Hämtat från: http://www.edusci.umu.se/np/np-2-4/resultat/ den 25 mars 2016.
Skolverket (2015b). Resultat från nationellt kursprov i Matematik 2abc, våren 2015, samt
lärarenkät. Hämtat från: http://www.edusci.umu.se/np/np-2-4/resultat/ den 25 mars 2016.
Storbacka, Jenni-Marie (2011). Icke godkänt i matematik. En kartläggning av
gymnasieelevers kunskaper i plangeometri. (Rapport nr: 2011ht4969). Uppsala: Institutionen
för pedagogik, didaktik och utbildningsstudier, Uppsalas universitet. Tillgänglig:
http://uu.diva-portal.org/smash/get/diva2:534032/FULLTEXT01.pdf
Szabo, A., Larson, N., Viklund, G., Dufåker, D. & Marklund, M. (2012). Matematik Origo
2b. Stockholm: Sanoma Utbildning.
Tambour, T.(2002). Euklidisk geometri. Tillgänglig:
http://www.math.chalmers.se/Math/Grundutb/CTH/mve365/1415/Geometri_TT.pdf Hämtad
den 24 mars 2016.
Van Hiele, P. M. (1986). Structure and Insight. A theory of Mathematics Education.
Academic press Inc.
Vetenskapsrådet (2002). Forskningsetiska principer inom humanistisk-samhällsvetenskaplig
forskning [Elektronisk resurs]. Stockholm: Vetenskapsrådet.
32
Bilaga 1. Kunskapstest
1.
a) Bestäm vinkeln x
b) Vilket eller vilka av följande geometriska samband använde du då du bestämde vinkeln x?
Endast svar fordras
A. Pythagoras sats
B. Vinkelsumman i en triangel är 180°
C. Summan av sidovinklar är 180°
D. Yttervinkelsatsen
E. Topptriangelsatsen
F. Randvinkelsatsen
(NpMaB vt 2005 Version 1)
2. Två likformiga rektanglar har olika mått. Rektangel A har sidorna 4 cm och 6 cm.
Rektangel B har en sida som är 12 cm.
Vilka mått kan den andra sidan hos rektangel B ha?
3. Punkterna A, B och C ligger på en cirkel.
O är cirkelns medelpunkt. Bestäm vinklarna i triangeln
ABC.
Mätning i figur accepteras ej
(Np MaB vt 2002)
33
(NpMa2b vt 2012)
4. I den likbenta triangeln ABC är basen BC. Punkt M är mittpunkt på BC. Förklara
att trianglarna ABM och ACM är kongruenta.
A
B
M
C
5. Lina och Sara är ute och seglar i en båt som de har lånat. De seglar mot en bro och
börjar fundera på om masten är för hög för att båten ska kunna passera under bron. För
att kunna bestämma mastens höjd gör de några mätningar.
Lina och Sara mäter avståndet från mastens fot och rakt ut mot akterstaget och finner
att det är 4,50 m. Sedan mäter de avståndet från masten till akterstaget 0,80 m högre
upp och parallellt med första mätningen. Det avståndet är 4,20 m. Se figur.
Använd de mätningar som Lina och Sara har gjort och bestäm mastens höjd.
(NpMaB vt 2011)
34
Bilaga 2. Skolverkets korrekta lösningar av uppgift 1, 2, 3 och 5
Skolverket anger följande lösningar
Uppgift 1. (Skolverket, 2005, s. 13)
a) Redovisad godtagbar lösning (40°) (+1 g, g = Godkänd)
b) Korrekt svar utifrån lösningen i a) (t.ex. B och C) (+1 g, g = Godkänd)
Uppgift 2. (Skolverket, 2012b, s. 23)
Godtagbar ansats, visar förståelse för likformighetsbegreppet, t.ex. genom att
bestämma en tänkbar längd på sidan (+1 EB, B = Begrepp)
med i övrigt godtagbar lösning med korrekt svar (8 cm och 18 cm) (+1 EPL, PL =
Problemlösning)
Uppgift 3. (Skolverket, 2002, s. 10)
Redovisad godtagbar beräkning av en vinkel i triangeln ABC (+1 g, g = godkänd)
Redovisad godtagbar beräkning av ytterligare två vinklar i triangeln ABC (70º, 50º och 60º)
(+1 vg, vg = Väl godkänd)
Uppgift 5. (Skolverket, 2011b, s. 21)
Godtagbar ansats, t.ex. använder topptriangelsatsen korrekt (+1CM, M= Modellering)
med i övrigt godtagbar lösning med korrekt svar (12 m) (+1CM, M= Modellering)
35
Bilaga 3. Lösningsförslag till testet
Uppgift 1.
a)
Yttervinkelsatsen ger oss följande ekvation:
𝑥 + 1040 = 1440
𝑥 = 1440 − 1040
𝑥 = 400
Svar: Vinkeln 𝑥 är 400 .
Svar: D Yttervinkelsatsen.
b)
Uppgift 2.
Rektangel B har en sida som är 12 cm. Denna sida kan vara kortsidan eller långsidan. Detta
medför att rektangel B kan ligga på två olika sätt.
Fall 1: Långsidan är 12 cm och antag att kortsidan är x.
x
4 cm
Två likformiga rektanglar ger oss förhållandet
mellan motsvarande sidor följande ekvation:
B
A
6 cm
𝑥 12
=
4
6
12 cm
𝑥=8
Fall 2: Kortsidan är 12 cm och antag att långsidan är y.
B
Två likformiga rektanglar ger oss
förhållandet mellan motsvarande sidor
följande ekvation:
y
12 𝑦
=
4
6
12 cm
4 cm
A
6 cm
𝑦 = 18
Svar: Den andra sidan hos rektangel B kan vara 8 cm eller 18 cm.
36
Uppgift 3.
Randvinkeln BAC och medelpunktsvinkel BOC står på
den samma bågen BC. Enligt randvinkelsatsen har vi:
∧ 𝐵𝐴𝐶 =
∧ 𝐵𝑂𝐶 1400
=
= 700 .
2
2
Triangeln OCB är likbent (OB=OC), då har vi: ∧ 𝑂𝐵𝐶 =
∧ 𝑂𝐶𝐵.
Vi utnyttjar att vinkelsumma i triangeln OCB är 1800 och
får följande relation:
∧ 𝑂𝐵C +∧ 𝑂CB + 1400 = 1800.
Alltså är ∧ 𝑂𝐵C =∧ 𝑂CB =
1800−1400
2
= 200 .
Vinkeln ABC blir 300 + 200 = 500.
Vinkeln BCA blir: 1800 − (700 + 500 ) = 600 .
Svar: Vinkeln BAC är 700 , vinkeln ABC är 500 och vinkeln BCA är 600 .
Uppgift 4.
I trianglarna ABM och ACM har vi:
A
𝐴𝐵 = 𝐴𝐶 (eftersom ABC är likbent triangel med basen BC),
AM är gemensam sidan,
𝐵𝑀 = 𝐶𝑀 (eftersom M är mittpunkt på BC).
Enligt SSS kongruensfallet ger ∆𝐴𝐵𝑀 ≅ ∆𝐴𝐶𝑀.
B
C
M
Uppgift 5.
A
Antag mastens höjd är AC, avståndet från mastens fot och rakt
ut mot akterstaget är CB, avståndet från masten till akterstaget
är DE (se figuren).
Topptriangelsatsen ger oss: ∆𝐵𝐸𝐷~∆𝐵𝐶𝐴. Då har vi
𝐴𝐶
𝐵𝐶
förhållandet: 𝐷𝐸 = 𝐵𝐸 .
Vi ersätter 𝐵𝐶 = 4,50 𝑚, 𝐷𝐸 = 0,80 𝑚 och 𝐵𝐸 = 4,50 − 4,20 =
0,30 𝑚 och får
D
𝐴𝐶
0,8
4,20
Alltså är 𝐴𝐶 = 15 ∙ 0,8 = 12.
0,80
B
E 4,50
4,50
= 0,30 = 15.
C
Svar: Mastens höjd är 12 m.
37
Bilaga 4. De grundläggande klassiska satserna inom geometri
I denna bilaga presenteras många av definitioner och satser om vinklar, kongruenta trianglar
och likformiga trianglar som elever i kursen matematik 2b behöver använda.
1. Vinklar.
Nedanför sammanfattas vinklar som är hämtat ifrån Szabo, Larson, Viklund, Dufåker
& Marklund (2012).
Sats 1. Vinkelsumman i en triangel är 1800 .
x
𝑥 + 𝑦 + 𝑧 = 1800
y
z
Om två linjer skär varandra så uppstår fyra vinklar. Vilket vi kan se i den här figuren:
v
w
u
t
Vinklar med gemensamt vinkelben, som u och v i figuren, kallas sidovinklar. Vinkelsumman
av två sidovinklar är alltid lika med 1800 . I figuren 𝑢 + 𝑣 = 1800 .
Ett par av dessa vinklar som inte har något gemensamt vinkelben kallas vertikalvinklar.
Vertikalvinklar är alltså lika. I figuren vertikalvinklar 𝑢 = 𝑤 och 𝑣 = 𝑡.
En linje som skär två linjer l och l’ i nästa figur kallas en transversal.
l
y
x
v
l'
u
38
Vinklarna u och x respektive v och y kallas likbelägna medan u och y respektive v och x kallas
alternatvinklar.
Om l och l’ är parallella så är likbelägna respektive alternatvinklar lika stora.
En yttervinkel till en triangel är en sidovinkel till en av de vinklarna i triangeln.
Sats 2. (Yttervinkelsatsen). En yttervinkel till en triangel är lika med summan av de
motstående innervinklarna.
x
𝑢 = 𝑥+𝑦
y
u
Sats 3. (Randvinkelsatsen). I en cirkel är medelpunktsvinkeln dubbelt så stor som
randvinkeln på samma cirkelbåge.
R
𝑤 = 2𝑣
v
M
w
B
A
Följdsatser till randvinkelsatsen.
1. Randvinklar till samma cirkelbåge är lika stora.
2. Randvinklar till en halvcirkelbåge är räta vinklar.
3. I en fyrhörning inskriven i en cirkel är summan av motstående vinklar 1800 .
2. Kongruens
I detta avsnitt kommer jag att presentera kongruenta trianglar och tre kongruensfall som är
hämtat ifrån Tambour (2002).
Två kongruenta trianglar ∆𝐴𝐵𝐶 och ∆𝐴′𝐵′𝐶′ har två viktiga egenskaper hos följande:
* Motsvarande sidor är lika: |𝐴𝐵| = |𝐴′ 𝐵′ |, |𝐵𝐶| = |𝐵′ 𝐶 ′ |, |𝐴𝐶| = |𝐴′ 𝐶′|.
* Motsvarande vinklar är lika: ∧ 𝐴 =∧ 𝐴′ , ∧ 𝐵 =∧ 𝐵′ , ∧ 𝐶 =∧ 𝐶 ′ .
39
A'
A
B
C
B'
C'
Kongruens betecknas: ∆𝐴𝐵𝐶 ≅ ∆𝐴′𝐵′𝐶′.
För att bevisa att två trianglar är kongruenta brukar man använda en av de tre kongruensfall:
Första kongruensfallet (ofta kallat SVS, sida-vinkel-sida): Om i två trianglar ∆𝐴𝐵𝐶 och ∆𝐴′𝐵′𝐶′
gäller att |𝐴𝐵| = |𝐴′ 𝐵′ |, ∧ 𝐴 =∧ 𝐴′ , och |𝐶𝐴| = |𝐶 ′ 𝐴′ |, så är ∆𝐴𝐵𝐶 ≅ ∆𝐴′𝐵′𝐶′.
Andra kongruensfallet (SSS): Om i två trianglar ∆𝐴𝐵𝐶 och ∆𝐴′𝐵′𝐶′ gäller att |𝐴𝐵| = |𝐴′ 𝐵′ |,
|𝐵𝐶| = |𝐵′ 𝐶 ′ | och |𝐴𝐶| = |𝐴′ 𝐶′|, så är ∆𝐴𝐵𝐶 ≅ ∆𝐴′𝐵′𝐶′.
Tredje kongruensfallet (VSV): Om i två trianglar ∆𝐴𝐵𝐶 och ∆𝐴′𝐵′𝐶′ gäller att ∧ 𝐴 =∧ 𝐴′ , |𝐴𝐵| =
|𝐴′ 𝐵′ | och ∧ 𝐵 =∧ 𝐵′ , så är ∆𝐴𝐵𝐶 ≅ ∆𝐴′𝐵′𝐶′.
I boken ”Matematik Origo 2b” har Szabo m.fl. (2012) också definierat kongruenta
månghörningar.
40
3. Likformighet
I detta avsnitt presenteras likformiga trianglar, tre likformighetsfall, topptriangelsatsen och
bisektrissatsen som är hämtat från Tambour (2002). Transversalsatsen presenteras också och
hämtats från Szabo, Larson, Viklund, Dufåker & Marklund (2012).
Två likformiga trianglar ∆𝐴𝐵𝐶 och ∆𝐴′𝐵′𝐶′ har två viktiga egenskaper hos följande:
* Motsvarande vinklar är lika: ∧ 𝐴 =∧ 𝐴′ , ∧ 𝐵 =∧ 𝐵′ , ∧ 𝐶 =∧ 𝐶 ′ .
* Likformighetsskalan:
|𝐴𝐵|
|𝐴′ 𝐵′ |
|𝐴𝐶|
|𝐵𝐶|
= |𝐴′ 𝐶′| = |𝐵′ 𝐶 ′ |
A'
A
B'
C'
C
B
Likformighet betecknas: ∆𝐴𝐵𝐶~∆𝐴′𝐵′𝐶′.
För att bevisa två trianglar är likformiga brukar man använder en av de tre likformighetsfall:
Första likformighetsfallet (SVS): Om i två trianglar ∆𝐴𝐵𝐶 och ∆𝐴′𝐵′𝐶′ gäller att
|𝐴𝐵|
|𝐴′ 𝐵′ |
|𝐴𝐶|
= |𝐴′ 𝐶′|
och ∧ 𝐴 =∧ 𝐴′ , så är ∆𝐴𝐵𝐶~∆𝐴′𝐵′𝐶′.
Andra likformighetsfallet (SSS): Om i två trianglar ∆𝐴𝐵𝐶 och ∆𝐴′𝐵′𝐶′ gäller att
|𝐵𝐶|
|𝐵′ 𝐶 ′ |
|𝐴𝐵|
|𝐴′ 𝐵′ |
|𝐴𝐶|
= |𝐴′
𝐶′|
=
, så är ∆𝐴𝐵𝐶~∆𝐴′𝐵′𝐶′.
Tredje likformighetsfallet (VV): Om i två trianglar ∆𝐴𝐵𝐶 och ∆𝐴′𝐵′𝐶′ gäller att ∧ 𝐴 =∧ 𝐴′ och
∧ 𝐵 =∧ 𝐵′ , så är ∆𝐴𝐵𝐶~∆𝐴′𝐵′𝐶′.
Sats 4. (Topptriangelsatsen). Varje topptriangel som bildas av en parallelltransversal är
likformig med hela triangeln.
A
D
B
E
∆𝐴𝐷𝐸~∆𝐴𝐵𝐶
C
Sats 5. (Bisektrissatsen). En bisektris i en triangel delar motstående sida enligt förhållandet
41
A
|𝐶𝐷| |𝐴𝐶|
=
|𝐵𝐷| |𝐴𝐵|
B
C
D
I boken ”Matematik Origo 2b” har Szabo m.fl. (2012) också definierat likformiga
månghörningar. Szabo et al. ger ytligare transversalsatsen.
Sats 6. (Transversalsatsen). En parallelltransversal delar två sidor i en triangel enligt samman
förhållande.
A
a
D
b
B
c
𝑎
𝑏
E
d
𝑐
= 𝑑 eller
𝑏
𝑎
=
𝑑
𝑐
C
42