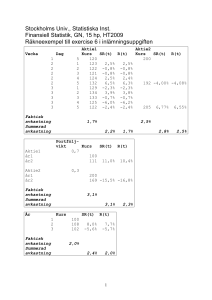
σ σ ρ σ σ ρ
advertisement

Formelsamling - finansiell ekonomi Förväntad avkastning på en portfölj N E( rp ) = ∑ X i ri i =1 X i = vikt för tillgång i ri = avkastning på tillgång i Kovarians i avkastning mellan två tillgångar Kovi , j = ρ i , jσ iσ j ρ i , j = korrelatio n i avkastning mellan tillgång i och j σ i = standardavvikelsen i avkastning en för tillgång i σ j = standardavvi kelsen i avkastning en för tillgång j Standardavvikelsen i avkastningen för en portfölj som består av 2 tillgångar [ σ p = X 12 σ12 + X 22 σ 22 + 2 X 1 X 2ρ1,2σ1σ 2 ] 1/ 2 X 1 = vikt för tillgång 1 σ1 = standardavvikelsen i avkastning för tillgång 1 X 2 = vikt för tillgång 2 σ 2 = standardavvikelsen i avkastning för tillgång 2 ρ1,2 = korrelation i avkastning mellan tillgång 1 och 2 Marknadsmodellen ri = α i + βi RM + ε i α i = företagsspecifik avkastning för tillgång i βi = marknadsrisk (" beta" ) för tillgång i RM = avkastning på marknadsindex (" marknadsportföljen" ) ε i = en felterm för tillgång i Marknadsrisk βi = Kovi ,M σ 2M Kovi ,M = kovarians i avkastning mellan tillgång i och marknadsportföljen σ 2M = varians i avkastning för marknadsportföljen Varians för en placeringstillgång σi2 = βi2 σ 2M + σ ε2,i βi = marknadsrisk för tillgång i σ 2M = varians i avkastning för marknadsportföljen σ ε2,i = varians i feltermen för tillgång i Marknadsrisk för en portfölj N β p = ∑ X i βi i =1 X i = vikt för tillgång i βi = marknadsrisk (beta) för tillgång i CAPM-ansatsen E( Ri ) = R f + βi ( E( RM ) − R f ) R f = avkastning på det riskfria placeringsalternativet βi = marknadsrisk (beta) för tillgång i E(RM ) = förväntad avkastning på marknadsportföljen Diskonteringsmodellen - evigt kassaflöde D1 r D1 = förväntad aktieutdelning V= r = avkastningskrav Diskonteringsmodellen - konstant tillväxt D1 (r −g ) D1 = förväntad aktieutdelning V= r = avkastningskrav g = tillväxttakt Köp/sälj partiteten X (1 + r ) C = pris på en köpoption P = pris på en säljoption X = lösenpris S =C−P+ Treynors utvärderingsmått T= Rp − R f βp R p = avkastning på portföljen R f = avkastning på det riskfria placeringsalternativet β p = portföljens marknadsrisk Sharpes utvärderingsmått S= Rp − R f σp R p = avkastning på portföljen R f = avkastning på det riskfria placeringsalternativet σ p = s tan dardavvikelse i portföljens avkastning