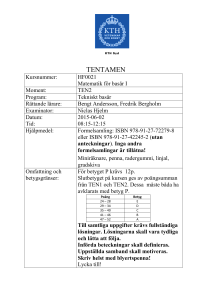
Nollproduktsmetoden ger att

TENTAMEN
Kursnummer:
Moment:
Program:
Rättande lärare:
Examinator:
Datum:
Tid:
Hjälpmedel:
Omfattning och
betygsgränser:
HF0021
Matematik för basår I
TEN2
Tekniskt basår
Niclas Hjelm, Sara Sebelius & Håkan
Strömberg
Niclas Hjelm
2015-12-14
08:15-12:15
Formelsamling: ISBN 978-91-27-72279-8
eller ISBN 978-91-27-42245-2 (utan
anteckningar). Inga andra
formelsamlingar är tillåtna!
Miniräknare, penna, radergummi, linjal,
gradskiva
För betyget P krävs 12p.
Slutbetyget på kursen ges av poängsumman
från TEN1 och TEN2. Dessa måste båda ha
avklarats med betyg P.
Poäng
24 – 28
29 – 34
35 – 40
41 – 46
47 – 52
Betyg
E
D
C
B
A
Till samtliga uppgifter krävs fullständiga
lösningar. Lösningarna skall vara tydliga
och lätta att följa.
Införda beteckningar skall definieras.
Uppställda samband skall motiveras.
Skriv helst med blyertspenna!
Lycka till!
Student som är godkänd på KS4 hoppar över uppgift 1-4
x3
1. Bestäm f ´(1) om f ( x ) 
 0,5 x
2
(2p)
2. Beräkna f´(x) med hjälp av derivatans definition då f ( x )  x 2  5x
(2p)
3. Bestäm eventuella extrempunkter till funktionen y ( x ) 
e 2 x  x
1
3
4. Bestäm det största och minsta värdet för funktionen f ( x)  x 3 
i intervallet  3  x  1
(2p)
9x 2
 6x  4
2
(2p)
Dessa uppgifter gör alla
5. Under gynnsamma förhållanden kan en viss typ av bakterier tillväxa enligt formeln
N ( x )  N 0  2 ( 3 x ) där N 0 är antalet bakterier från början och N är antalet bakterier efter x
timmar.
Antag att vi startar med 1 bakterie med massan 1,0  10 12 g samt att tillväxten kan ske utan
begränsningar. Hur lång tid tar det innan bakteriemassan är lika stor som jordens nuvarande
massa på 6,0  10 24 kg?
(2p)
6. En cirkel har medelpunkt i (-5, 8) och har radien 7.
En punkt på cirkeln är (2,k), Bestäm talet k.
(2p)
7. Bestäm sidorna i en liksidig triangel med arean 84,0 cm2.
(2p)
8. Bestäm sträckan AB i figuren nedan.
(2p)
9. Funktionen y( x )  x 3  1,5x 2 har en lokal maximipunkt. I denna punkt dras en tangent
som skär kurvan i ytterligare en punkt. Beräkna den andra punktens koordinater. (2p)
10. Lös ekvationen
lg( 5 x  6)  lg( 2 x  1)  lg x
(2p)
11. Vid djupfrysning av en maträtt kyls maten enligt formeln
f (t )  Be kt  30
där f C är matens temperatur då kylningen pågått i t minuter. När maten kylts i 5,0
minuter är dess temperatur 78 C och efter 8,0 min har temperaturen hos maten sjunkit till
71° C. Vid vilken tidpunkt sjunker temperaturen med 2,1 °C/min?
(3p)
12. Ett kärl utan lock har formen av ett rätblock med kvadratisk bottenyta. Hur mycket kan
ett sådant kärl maximalt rymma om dess begränsningsarea är 9,0 dm²?
(3p)
Förslag till lösningar:
x3
x 3 x 0,5
 0,5 x 

2
2
2
2
3x
1
f ´( x ) 

2
4 x
Villkoret f ´(1) ger:
1. f ( x ) 
3  12
1
3 1 5

  
2
4 1 2 4 4
5
Svar: f ´(1) 
4
f ´(1) 
2. Derivatans definition
f ( x  h)  f ( x )
då f ( x )  x 2  5x ger:
f ( x)  lim
h 0
h
( x  h ) 2  5( x  h )  ( x 2  5 x )
x 2  2 xh  h 2  5 x  5h  x 2  5 x
 lim

h 0
h 0
h
h
2 xh  5h  h 2
lim
 lim ( 2 x  5  h )  2 x  5
h 0
h 0
h
f ´( x )  lim
Svar: f ´( x )  2 x  5
3. För att ta reda på funktions ev. extrempunkter deriveras funktion och y´( x )  0 :
 2e 2 x  1
y´( x ) 
3
y´( x )  0
Vilket ger
 2 e 2 x  1
0
3
2 x
0  2 e  1
1
  e 2 x
2
Denna ekvation saknar reella lösningar, dvs funktionen har inga extrempunkter.
Svar: Funktionen saknar extrempunkter.
4. För att ta reda på funktions ev. extrempunkter deriveras funktion och f ´( x)  0 :
f ´( x)  3x 2  9 x  6
f ´( x)  0
Vi får :
0  3x 2  9 x  6
0  3( x 2  3x  2)
Nollproduktsmetoden ger att
x 2  3x  2  0
Vilket ger lösningarna med pq-formeln:
3
3
3 1
x    ( )2  2   
2
2
2 2
x1  1
x 2  2
Båda dessa extrempunkter ligger inom intervallet och behöver kontrolleras. Insättning av
extrempunkter samt intervall gränser ger:
9(1) 2
13
f (1)  (1) 3 
 6(1)  4  
2
2
2
9(2)
f (2)  (2) 3 
 6(2)  4  6
2
9(3) 2
17
3
f (3)  (3) 
 6(3)  4  
2
2
2
9 1
15
f (1)  13 
 6 1  4 
2
2
Svar: Funktionens största och minsta värde i intervallet är f (1) 
f (3)  
15
samt
2
17
.
2
5. Eftersom varje bakterie väger 1,0  10 12 g  1,0  10 15 kg kommer det att finnas
6,0  10 24
 6,0  10 39 st då bakteriernas massa är lika stor som jordens nuvarande
1,0  10 15
massa. N 0  1 enligt uppgift
Detta ger insatt i ekvationen för tillväxt:
6,0  10 39  1  2 3 x
N
ln( 6,0  10 39 )  ln( 2 3 x )
ln( 6,0  10 39 )  3 x ln 2
ln( 6,0  10 39 )
 44 h
3 ln 2
Svar: Det skulle ta ca 44 h för bakterierna att få lika stor massa som jorden har nu
om bakterierna kunde växa obegränsat.
x
6. Cirkelns ekvation kan skrivas som
( x  5) 2  ( y  8) 2  7 2
( x  5) 2  ( y  8) 2  49
Insättning av (2,k) ger:
(2  5) 2  (k  8) 2  49
49  ( k  8) 2  49
(k  8) 2  0
k 8
Svar: k=8
7. En liksidig triangel är likvinklig.
180o
Varje vinkel är
= 60o.
3
Låt triangelns sida vara x cm.
o
Areasatsen ger att arean är x  x  sin 60 = 84,0
2
x2 
3
= 84,0
22
336
x2 =
3
x =  336  13,9 cm
3
(x>0)
Svar: Sidorna är ungefär 13,9 cm långa.
8.
Vi bestämmer vinkeln v i triangeln ABC med cosinussatsen.
Insättning av givna värden ger
4,52  8,02  7,32  2·8,0·7,3·cos v
8, 02  7,32  4,52
cos v 
2  8, 0  7,3
v  cos 1 (
8,02  7,32  4,52
)  33,8....
2  8,0  7,3
Cosinussatsen i triangeln RSB ger
RS2  3,02  5,62  2·3,0·5,6·cos 33,8…..o
RS   3,02  5,62  2  3,0  5,6  cos 33,8.....  3,528 cm (RS>0)
Svar: 3,5 cm
9. Tangenten till y ( x )  x 3  1,5x 2 söks:
y´( x)  3x 2  3x
Eftersom tangenten skär i en maximipunkt sätts kurvans derivata till noll:
0  3x 2  3x
0  3x( x  1)
Nollproduktsmetoden ger lösningarna x=0 samt x=1
För att undersöka vilken av punkterna som är en maximipunkt används andraderivatan:
y´´( x )  6 x  3
y´´(0)  3
y´´(1)  6  3  3
Vilket ger att x=0 är ett maximum eftersom y´´<0
Insättning av x=0 i funktinen ger:
y(0)  0 3  1,5  0 2  0
Tangentens ekvation blir då:
y(x)=0
Vi söker skärningspunkten mellan tangenten och kurvan:
 y( x)  0
 0  x 3  1,5x 2

3
2
 y ( x )  x  1,5x
Ekvationen faktoriseras:
0  x 2 ( x  1,5)
Nollproduktsmetoden ger lösningarna x=0 (vilket är max. punkten ) samt x=1,5
y-koordinaten för denna punkt beräknas:
y(1,5)  1,53  1,5  1,5 2  0
Svar: Skärningspunkternas koordinater är (1,5;0)
10. lg( 5 x  6)  lg( 2 x  1)  lg x
(x>0)
Omskrivning med logaritmlagarna ger:
lg( 5 x  6)  lg( x ( 2 x  1))
5x  6  2 x 2  x
0  2x2  4x  6
0  1( x 2  2 x  3)
Nollproduktsmetoden ger lösningarna kan skrivas som
0  x2  2x  3
Pq-formeln ger:
x  1  12  3  1  2
x1  3
x 2  1
Lösningen x  1 tillhör inte definitionsmängden.
Svar: Ekvationen har lösningen x=3.
11. f (t )  Be kt  30
För att kunna använda ekvationen måste först k och B bestämmas:
f (5)  78 ger sambandet:
f (5)  Be 5k  30
78  Be 5k  30
108  Be 5k
B
108
e 5k
f (8)  71
f (8)  Be
ger sambandet:
8k
 30
71  Be 8k  30
101  Be 8k
101
e 8k
Dessa villkor ger tillsammans ekvationen:
B
108 101
 8k
e 5k
e
8k
e
101

5k
e
108
101
e 3k 
108
101
)
108
101
3k  ln(
)
108
k  ln( 101 / 108) / 3
Vi får då:
f (t )  Be (ln(101/108) / 3)t  30 .
Villkoret
y (5)  78 ger B:
ln e 3k  ln(
78  Be (ln(101/108) / 3)5  30  B  120,76
Formeln kan då skrivas:
f (t )  120,76e(ln(101/108) / 3) t  30
Vi söker t då f ´( t )  2,1C / min
y (t ) 
ln( 101 / 108)
 120,76e (ln(101/ 108) / 3) t
3
 2,1  2,6974e (ln(101/ 108) / 3) t
0,77852  e (ln(101/ 108) / 3) t
ln 0,77852 
ln( 101 / 108)
t
3
t  11,2
Svar: Efter ungefär 11 min sjunker hastigheten med 2,1°C/min.
12. Kalla bottenareans sidor för x samt höjden för h.
Vi får då ett uttryck för volymen:
V  x2h
(1)
Begränsningsarean kan tecknas som:
A  x 2  4  x  h där A=9,0 dm² enligt uppgift. Inättning i (1) ger:
9,0  x 2  4 xh
9,0  x 2  4 xh
9,0  x 2
h
4x
Insättning i (1) ger:
2
9,0
1
2
2 9,0  x )
V x hx (

x  x3 ( 0  x  3 )
4x
4
4
Vi söker den maximala volymen. V´(x) beräknas och sätts lika med noll:
9,0 3x 2
V ´( x) 

4
4
9,0 3 x 2
V ´( x)  0  0 

4
4
2
9,0  3 x
9,0
 x2
3
x   3 cm
Den negativa lösningen förkastas eftersom den inte ligger inom def. mängden.
Verifiering av extrempunkten är en max. punkt med hjälp av andra derivata:
6x
V ´´(x)  
4
V ´´( 3 )  0
Dvs. det är en max. punkt
Den maximala volymen blir då:
9,0
( 3)3 9 3  3 3 3 3
V ( 3) 
 3


 2,598 dm³
4
4
4
2
Svar: Den maximala volymen är 2,6 dm³.
Rättningsmall
Generella riktlinjer för tentamensrättning
Varje beräkningsfel
(Därefter fortsatt rättning enligt nya förutsättningar)
Beräkningsfel; allvarliga och/eller leder till förenkling
Prövning istället för generell metod
Felaktiga antaganden/ansatser
-1 poäng
Lösning svår att följa och/eller Svaret framgår inte tydligt
Om ’=’ saknas (t.ex. ’=>’ används istället)
Om ’=’ används felaktigt (t.ex. istället för ’=>’)
-1 poäng eller mer
-1 poäng/tenta
-1 poäng/tenta
Teoretiska uppgifter:
Avrundat svar
-1 poäng/tenta
Tillämpade uppgifter:
Enhet saknas/fel
Avrundningar i delberäkningar som ger fel svar
Svar med felaktigt antal värdesiffror ( ±1 värdesiffra ok)
-1 poäng/tenta
-1 poäng/tenta
-1 poäng/tenta
-2 poäng eller mer
- samtliga poäng
- samtliga poäng
Preliminära riktlinjer för specifika uppgifter
1. Korrekt deriverat
2. Använder inte derivatans definition
𝑓´(𝑥) = lim
ℎ→0
lim
h0
𝑓(𝑥+ℎ)−𝑓(𝑥)
+1p
-2p
framgår ej
-1p
kvar för länge (även när h satts till noll)
-1p
ℎ
3. Fel deriverat
4. Undersöker bara derivatans nollställen
Undersöker inte intervallgränser/extrempunkter
5. enhetsfel (t ex Löser systemet N(0)=1 N(t)=6*10^24)
6. Korrekt uppställd ekvation för cirkeln
7. -----
-2p
-1p
-1p/x-värde
-1p
+1p
8. Korrekt beräknad vinkel v
+1p
9. Tangentens ekvation hittas via maxpunkten och framgår tydligt.
Verifiering av max saknas.
+1p
-1p
10. Kontrollerar inte lösningarna
-1p
11. Korrekt beräknade konstanter
+1p
12. Korrekt uppställd volym i en variabel
Definitionsmängd saknas
Verifiering av Max saknas
+1p
-1p
-1p