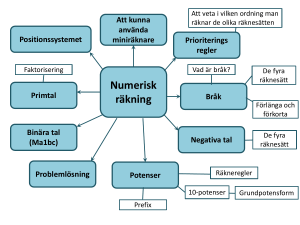
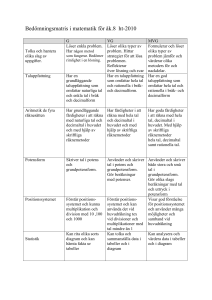
Vad är potensform?
advertisement

Vad är en potens? Om flera likadana faktorer multipliceras så kan produkten skrivas som en potens: är potensen och den består av en bas, 4, och en exponent, 3. Basen är den faktor som används i multiplikationen och exponenten anger antalet faktorer. utläses ”fyra upphöjt till tre”. Basen kan vara såväl tal i decimalform som negativa tal. Exempel: Exempel: Observera att inte är detsamma som : Räkneregler Vid räkning med potenser gäller ett antal räkneregler. För att dessa ska kunna formuleras på ett generellt sätt används nedan bokstäver för att beteckna tal. Multiplikation Exempel: Slutsats: Vid multiplikation av potenser med samma bas, adderas exponenterna. Regel: . . . Division Exempel: Observera att förkortas bort eftersom Slutsats: Vid division av potenser med samma bas, subtraheras exponenterna. Regel: Exponenten är noll Exempel: Observera att eftersom täljaren = nämnaren så är kvoten ett. Enligt tidigare räkneregel om division av potenser med samma bas så är det även möjligt att subtrahera exponenterna: Slutsats: En potens med exponenten noll är lika med ett. Regel: . . . . . . . . Negativ exponent Exempel: Observera att förkortas bort eftersom Enligt tidigare räkneregel om division av potenser med samma bas så är det även möjligt att subtrahera exponenterna: Slutsats: En potens med negativ exponent är lika med 1 dividerat med samma potens med positiv exponent. Regel: En potens där basen är en potens Exempel: Slutsats: En potens där basen är en potens är lika med en potens där exponenterna multipliceras med varandra. Regel: Sammanfattning Följande räkneregler gäller för potenser: 1. 2. 3. 4. 5. Tiopotenser Eftersom vi har ett talsystem med basen tio så är potenser med basen tio, så kallade tiopotenser, användbara för att på en enkelt sätt skriva stora och små tal. Exempelvis kan en miljard skrivas 109 eftersom På samma sätt kan en miljondel skrivas 10–6 eftersom Vidare kan exempelvis 7 000 000 skrivas som 7·106 eftersom 7·106 kan även skrivas som 70·105 Ett tal som skrivs som en produkt av ett tal i decimalform och en tiopotens med heltal exponent sägs vara skrivet i grundpotensform om talet i decimalform är större än eller lika med ett och samtidigt mindre än tio. 7·106 är skrivet i grundpotensform eftersom 7 är större än ett och mindre än tio. 70·105 är inte skrivet i grundpotensform eftersom 70 inte är mindre än tio. . . . . . . . . . . . . . . . . Fler exempel: Tal Skrivet med hjälp av Kommentar tiopotens 423 000 423·103 4,23·105 Ej grundpotensform. Grundpotensform. 105 000 000 105·106 1,05·108 Ej grundpotensform. Grundpotensform. 0,0000074 74·10-7 7,4·10-6 Ej grundpotensform. Grundpotensform. 1% 10-2 Faktorn 1 behöver inte skrivas före tiopotensen. 4,2 ‰ 4,2·10-3 ‰ = promille 5,2 ppm 5,2·10-6 ppm = miljondel 0,8 ppb 0,8·10-9 8·10-10 Ej grundpotensform. Grundpotensform. En bra minnesregel när tal skrivs med eller utan tiopotens är att antal förflyttningar av decimaltecknet motsvarar exponenten. Exempel: Decimaltecknet flyttas sex steg åt vänster från 5 800 000,0 till 5,8. Exempel: Decimaltecknet flyttas 13 steg åt höger från 0,00000000000078 till 7,8. 10-13